103. Имеются параллелограмм MNOP и трапеция MNEK с основанием EK, причём эти четырёхугольники не лежат в одной плоскости.
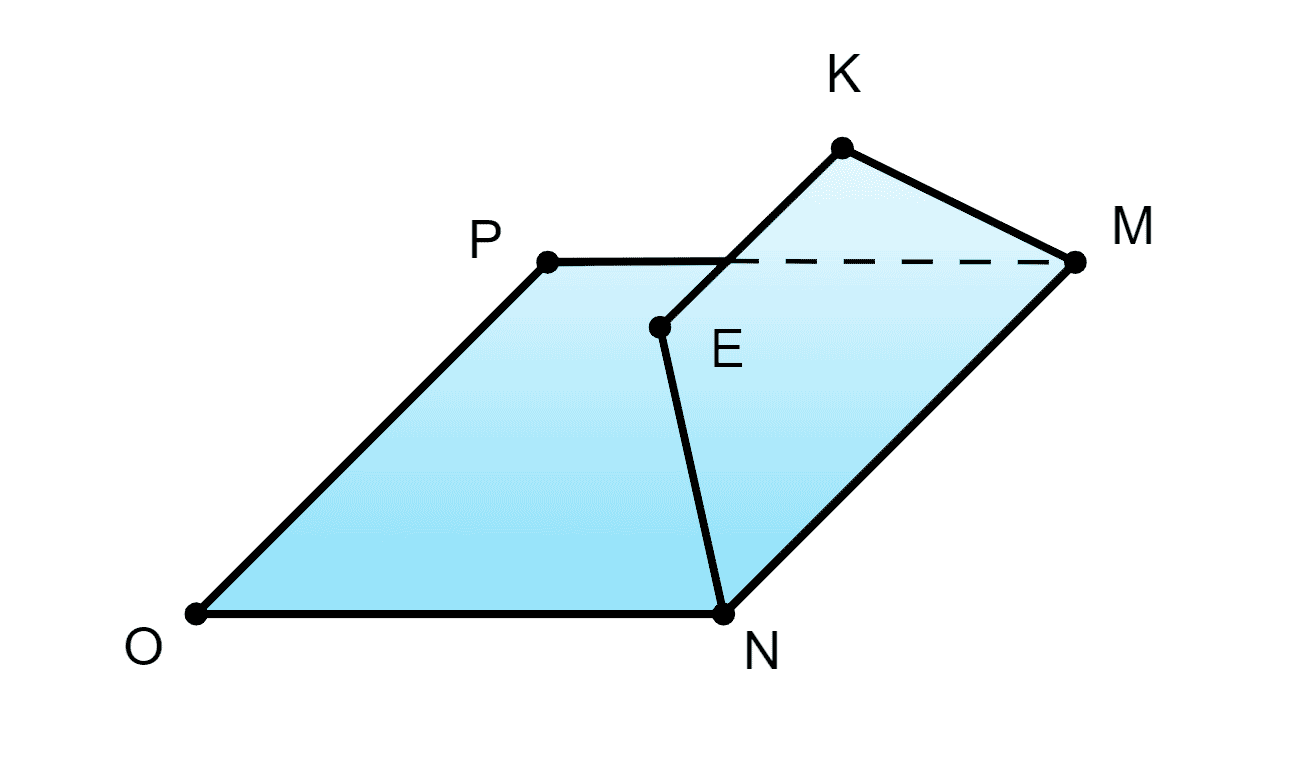
— трапеция, — параллелограмм.
а) Установите взаимное расположение прямых OP и EK.
По определению трапеции и параллелограмма имеем и
по Теореме 3
б) Найдите периметр трапеции, учитывая, что в неё можно вписать окружность, а её основания MN и EK равны 45 см и 55 см соответственно.
Т.к. в трапецию можно вписать окружность, то
Ответ: см.