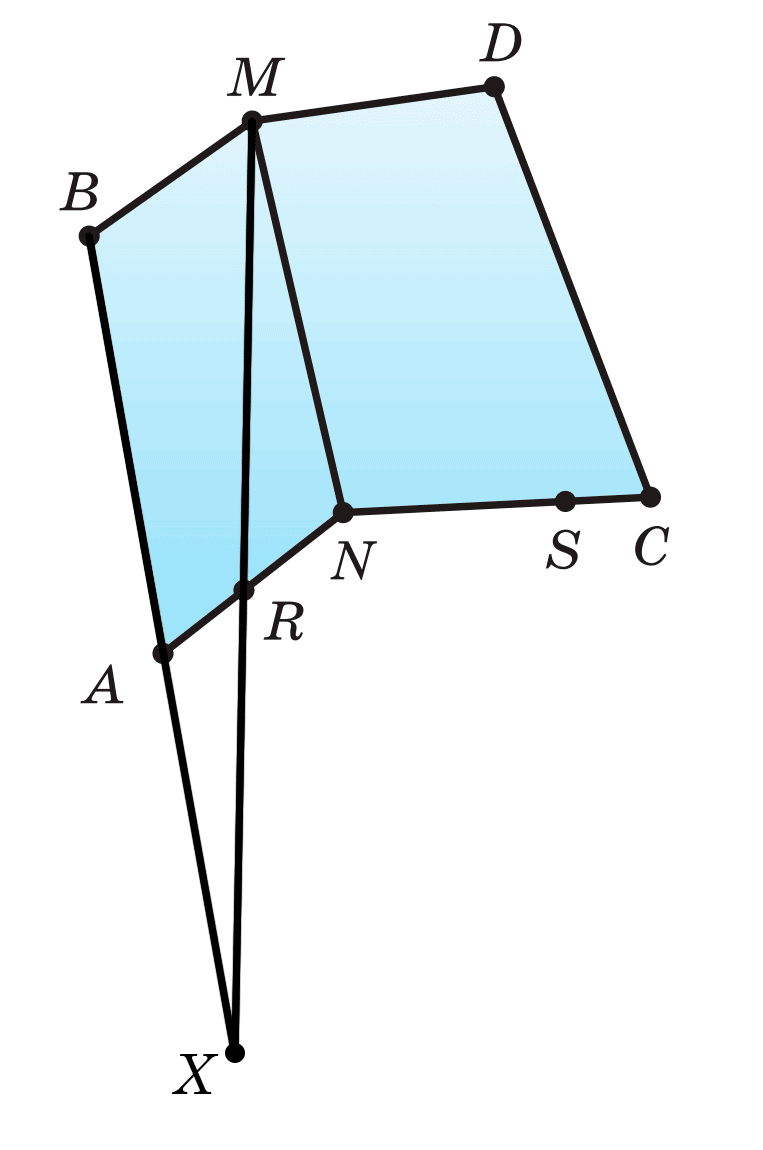
45. На отрезке MN как на стороне в разных плоскостях построены два четырёхугольника MNAB и MNCD, на отрезках NA и NC выбраны внутренние точки R и S соответственно (рис. 97). Сделайте такой рисунок в тетради и:

а) постройте точку, в которой прямая $MR$ пересекает плоскость $ABC.$

$MR\cap ABC=X$ ($MR$ пересекает $ABC$ в точке $X$)

б) постройте точку пересечения прямой $CD$ с плоскостью $ARS.$

Т.к. $(ARS)=(ANC)$ по Теореме 4 прямые $AN$ и $NC$ задают единственную плоскость, то $DC\cap (ARS)=C.$

в) докажите, что прямая $RS$ принадлежит плоскости $CAN.$

$RS\subset (CAN),$ т.к. $R\in (AN)$, $S\in (NC)$ и $(AN)\cap (NC),$ значит по Теореме 4 плоскость $CAN$ — единственная плоскость $\Rightarrow RS\subset (CAN).$