4. В прямоугольном треугольнике АВС гипотенуза АВ равна 25 см, катет АС равен 24 см. Найдите:

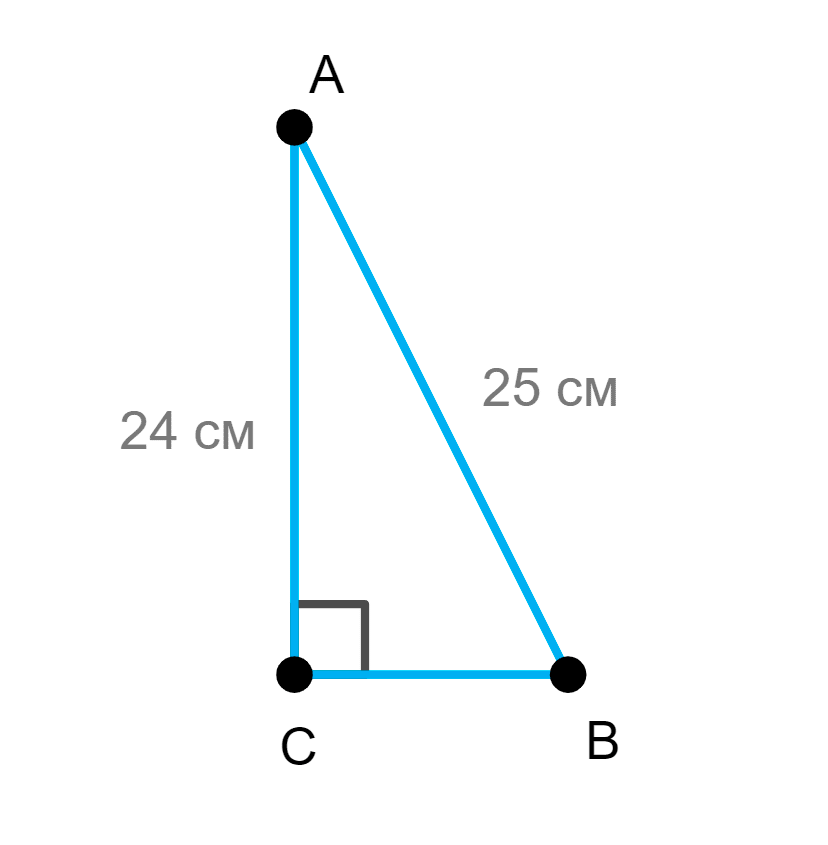
Найдём неизвестную сторону $BC.$ По теореме Пифагора $AC^2+BC^2=AB^2,$ значит $BC^2=AB^2-AC^2$

$BC=\sqrt{AB^2-AC^2}$

$BC=\sqrt{25^2-24^2}=\sqrt{625-576}=\sqrt{49}=7\,(см).$

а) $\sin{A}=\dfrac{BC}{AB}=\dfrac{7}{25};$

б) $\cos{A}=\dfrac{AC}{AB}=\dfrac{24}{25};$

в) $\tg{B}=\dfrac{AC}{CB}=\dfrac{24}{7};$

г) $\ctg{B}=\dfrac{BC}{AC}=\dfrac{7}{24};$

д) $\tg{B}\cdot\ctg{B}=\dfrac{AC}{CB}\cdot\dfrac{BC}{AC}=1;$

е) $\sin^2{A}+\cos^2{A}=\dfrac{7}{25}^2+\dfrac{24}{25}^2=\dfrac{7^2+24^2}{25}=1.$