Контр. 8. Соотношение между сторонами и углами прямоугольного треугольника

1. Треугольник $ABC$ [2 в.: $MNK$] — прямоугольный. Укажите верное равенство:

Вариант 1

а) $\text{tg}∠A=\frac{CB}{AB};$
б) $\cos ∠B=\frac{CB}{AC};$
в) $\sin ∠A=\frac{CB}{AB}.$

Ответ: а) $\text{tg}∠A=\frac{CB}{AB}.$

Вариант 2

а) $\text{ctg}∠K=\frac{KN}{MK};$
б) $\cos ∠M=\frac{MN}{MK};$
в) $\sin ∠K=\frac{MN}{KN}.$

Ответ: б) $\cos ∠M=\frac{MN}{MK}.$

2. Пользуясь данными рисунка, найдите косинус угла FPK [2 в.: $PFK$].

Вариант 1

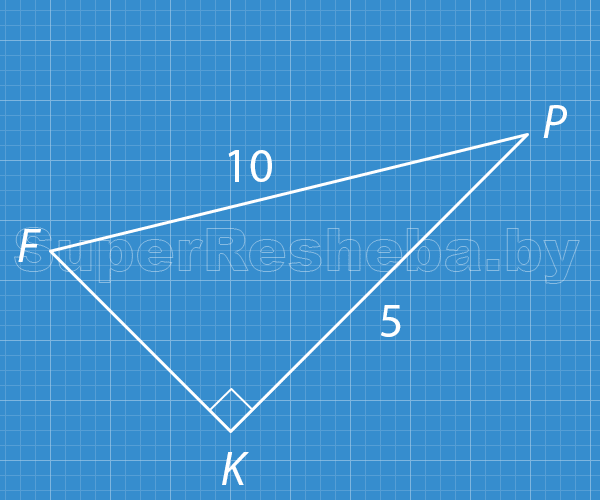
Ответ: $\dfrac{1}{2}.$

Вариант 2

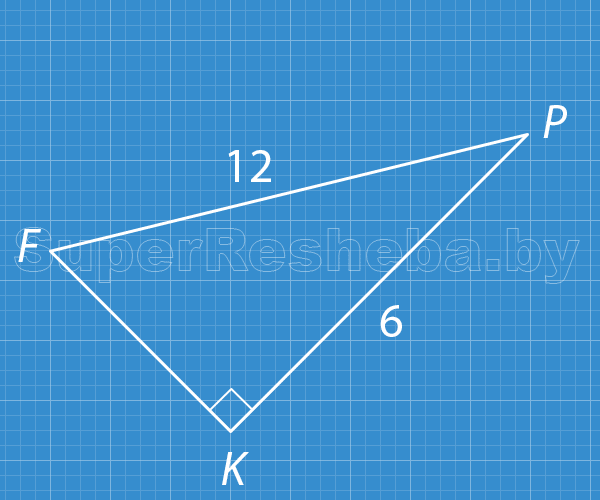
Ответ: $\dfrac{1}{2}.$

3. Вычислите:

Вариант 1

$\sin 30° - \text{ctg} 45° = \dfrac{1}{2} - 1 = -\dfrac{1}{2}.$

Вариант 2

$\text{tg} 45° - \cos 60° = 1 - \dfrac{1}{2} = \dfrac{1}{2}.$

4. Пользуясь данными рисунка, найдите синус [2 в.: косинус] угла PEM [2 в.: $CAB$].

Вариант 1

1. $ME = 13$ (по теореме Пифагора);
2. $\sin ∠PEM = \dfrac{MP}{ME} = \dfrac{5}{13}.$

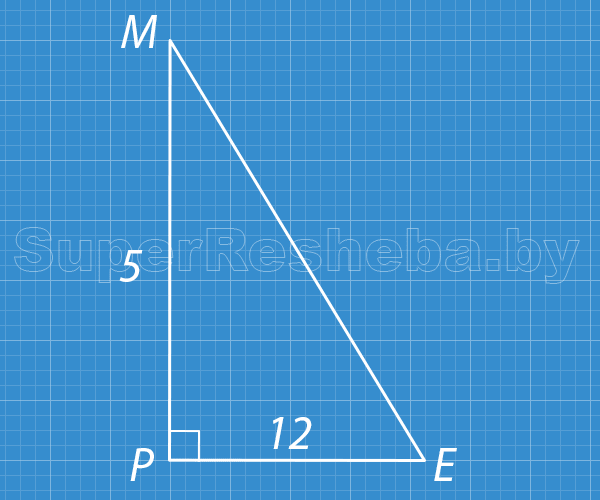
Ответ: $\dfrac{5}{13}.$

Вариант 2

1. $AB = 5$ (по теореме Пифагора);
2. $\cos ∠CAB = \dfrac{AC}{AB} = \dfrac{3}{5}.$

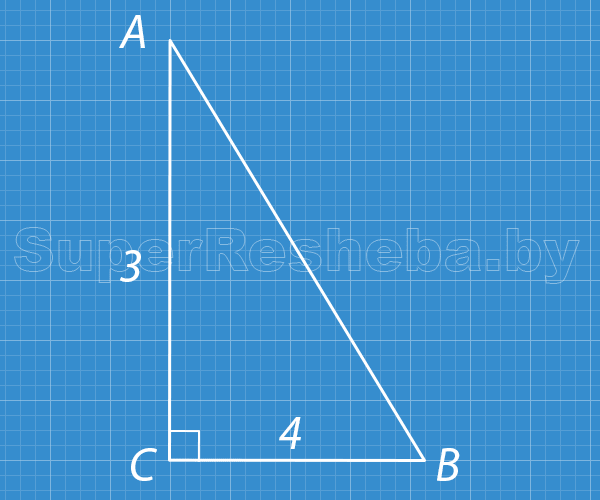
Ответ: $\dfrac{3}{5}.$

5. В прямоугольном треугольнике один из катетов равен $4$ см, а синус противолежащего ему угла равен $0.8.$ Найдите второй катет и гипотенузу этого треугольника.

Вариант 1

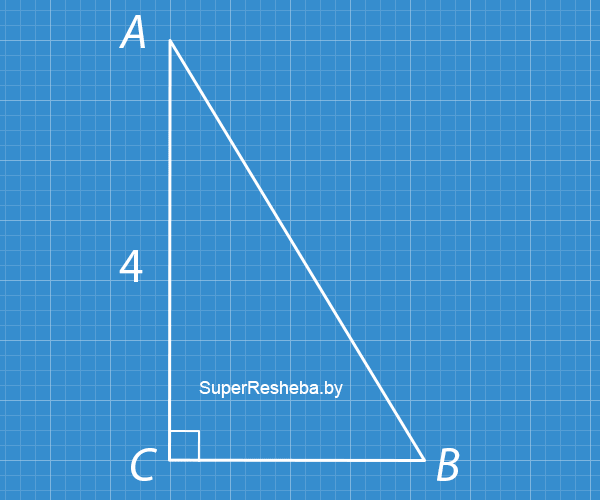
1. $\sin ∠ABC = 0.8 - \dfrac{5}{4},$ значит $\dfrac{AC}{AB} = \dfrac{5}{4},$ откуда $AB = 5\, (см);$
2. $CB = 3\, см$ (по теореме Пифагора).

Ответ: $3$ см.

Вариант 2

В прямоугольном треугольнике один из катетов равен $3$ см, а косинус прилежащего ему угла равен $0.6.$ Найдите второй катет и гипотенузу этого треугольника.

Решение

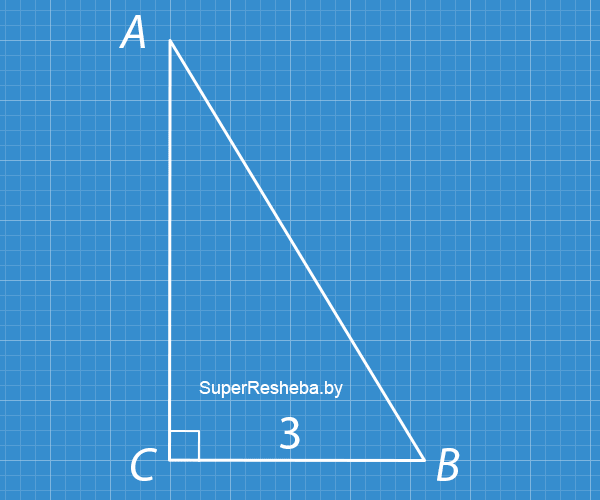
1. $\cos ∠ABC = 0.6 -\dfrac{5}{3},$ значит $\dfrac{CB}{AB} = \dfrac{5}{3},$ откуда $AB = 3\, (см);$
2. $AC = 4\, см$ (по теореме Пифагора).

Ответ: $4$ см.

6. Упростите выражение:

Вариант 1

$\text{tg}\alpha · \cos^2 \alpha + \cos^2(180°-\alpha)$ $=\dfrac{\sin^2\alpha · \cos^2\alpha}{\cos^2\alpha} + \cos^2(180°-\alpha)$ $=\sin^2(180°-\alpha)+\cos^2(180°-\alpha)=1.$

Вариант 2

$\text{ctg}\beta ·\sin^2\beta + \sin^2(180°-\beta)$ $=\dfrac{\cos^2\beta · \sin^2\beta}{\sin^2\beta} + \sin^2(180°-\beta)$ $=\cos^2\beta + \cos^2\beta = 1.$

7. Из вершины прямоугольника на диагональ опущен перпендикуляр, который делит её на отрезки длиной $9$ см и $16$ см. Найдите котангенс угла, образованного меньшей стороной и диагональю.

Вариант 1

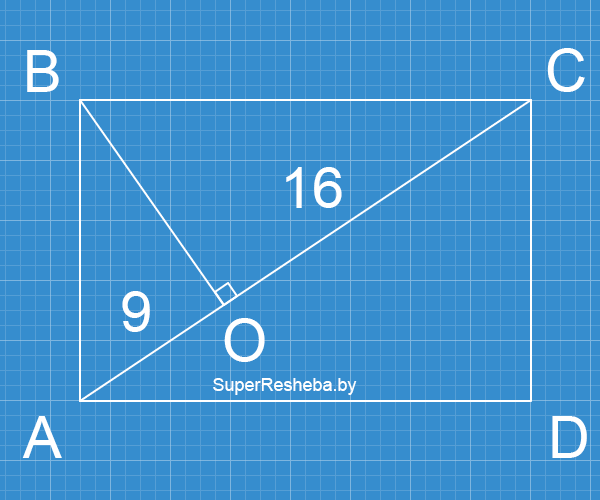
$ΔАОВ$ и $ΔАВС$ — подобны;
$\dfrac{9}{АВ} = \dfrac{АВ}{25};$
$АВ=15;$
$ВС=20;$
$\text{tg}=\dfrac{20}{15} = \dfrac{4}{3}.$

Ответ: $\dfrac{4}{3}.$

Вариант 2

Из точки пересечения диагоналей ромба проведён перпендикуляр, который делит сторону ромба на отрезки длиной $16$ см и $25$ см. Найдите котангенс угла, образованного стороной ромба и меньшей диагональю.

Решение

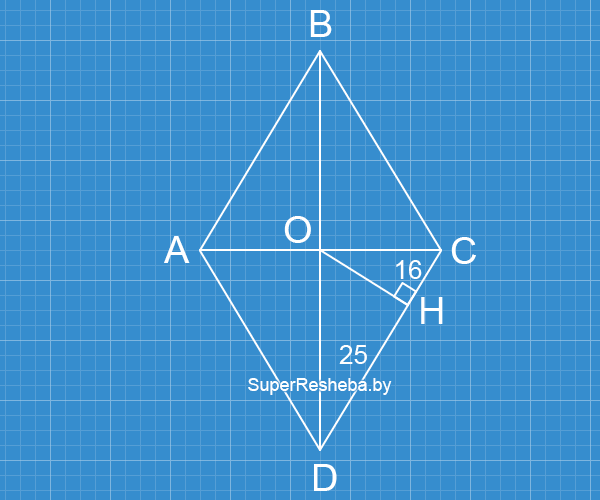
$ΔАОВ$ и $ΔАВС$ — подобны;
$\dfrac{16}{OC} = \dfrac{OC}{41};$
$АВ=15;$
$ВС=20;$
$\text{tg}=\dfrac{20}{15} = \dfrac{4}{3}.$

Ответ: $\dfrac{5}{4}.$

8. В прямоугольном треугольнике $MNK$ $∠M = 90°,$ $NK = 10,$ $\text{tg}∠K = 0.5.$ Найдите $MN$ и $MK.$

Вариант 1

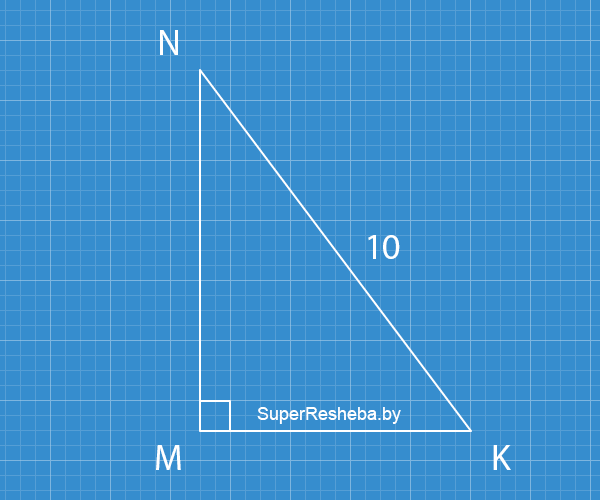
$\text{tg}∠K = 0.5 = \dfrac{1}{2},$ значит $MN:MK = 1:2,$ $MK = 2·MN.$

$(2x)^2 + x^2 = 10^2;$
$5x^2 = 100;$
$x^2 = 20;$
$x = 2\sqrt{5}.$

Ответ: $NM = 2\sqrt{5}, MK = 4\sqrt{5}.$

Вариант 2

В прямоугольном треугольнике $PST$ $∠S = 90°,$ $PT = 17,$ $\text{tg}∠P = 0.25.$ Найдите $PS$ и $ST.$

Решение

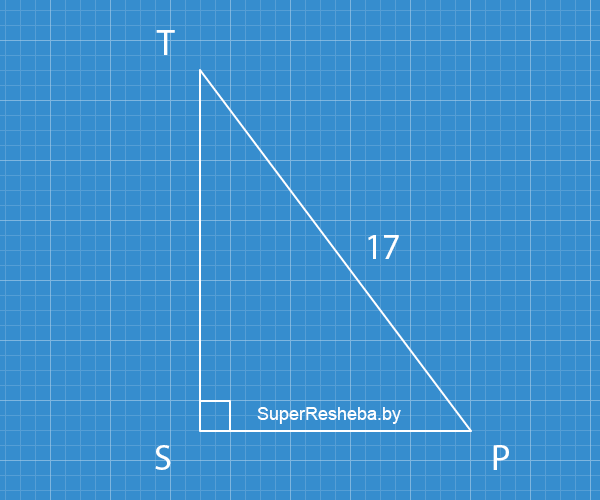
$\text{tg}∠P = 0.25 = \dfrac{1}{4},$ значит $TS:SP = 1:4,$ $SP = 4·TS.$

$(4x)^2 + x^2 = 17^2;$
$17x^2 = 289;$
$x^2 = 17;$
$x = \sqrt{17}.$

Ответ: $TS = \sqrt{17}, SP = 4\sqrt{17}.$

9. В параллелограмме $ABCD$ известно, что $AB = 17\, см$ и $BC = 10\, см,$ а $\text{tg}∠A = \frac{15}{8}.$ Найдите площадь параллелограмма.

Вариант 1

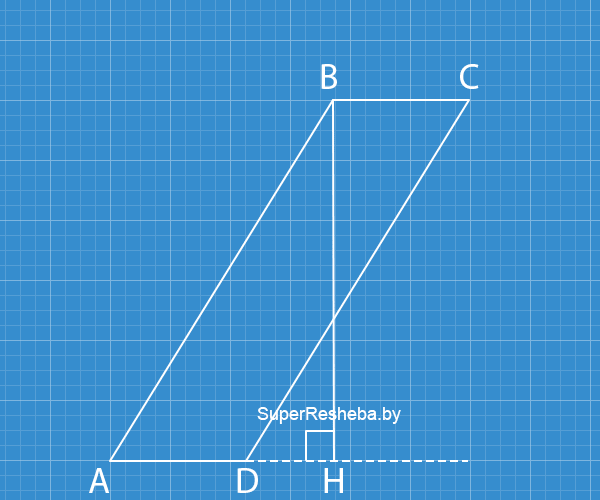
Так как $\text{tg}∠A = \dfrac{15}{8},$ то $BH = 15x;$ $AH = 8x.$

В треугольнике $ABH$ по теореме Пифагора получим $17^2= (8x)^2 + (15x)^2;$ $x = 1\, см.$

Тогда $BH = 15\, см$ и $S_{ABCD}$ $= AD · BH = 150\, см^2.$

Ответ: $150\, см^2.$

Вариант 2

В параллелограмме $MNPK$ известно, что $MN = 13\, см$ и $MK = 10\, см,$ а $\text{tg}∠M = \frac{15}{8}.$ Найдите площадь параллелограмма.

Решение

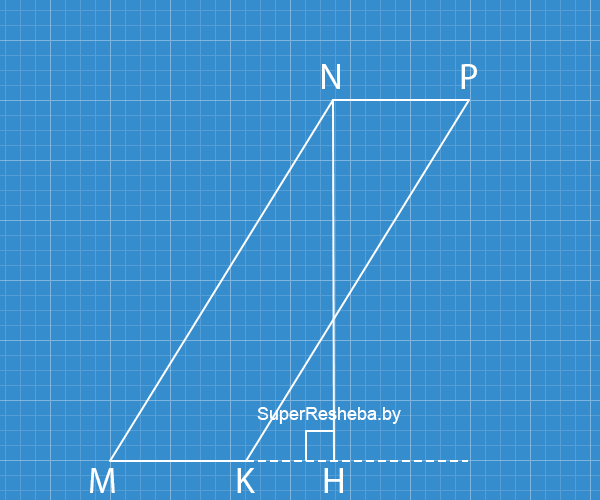
Так как $\text{tg}∠M = \dfrac{12}{5},$ то $MH = 12x;$ $MH = 5x.$

В треугольнике $MNH$ по теореме Пифагора получим $13^2= (12x)^2 + (5x)^2;$ $x = 1\, см.$

Тогда $NH = 12\, см$ и $S_{ABCD} = MK · NH = 120\, см^2.$

Ответ: $120\, см^2.$

10. Биссектриса $EP$ прямоугольного треугольника $MEH$ $(∠M = 90°)$ делит катет $MH$ в отношении $3 : 5.$ Найдите косинус угла $EHM.$

Вариант 1

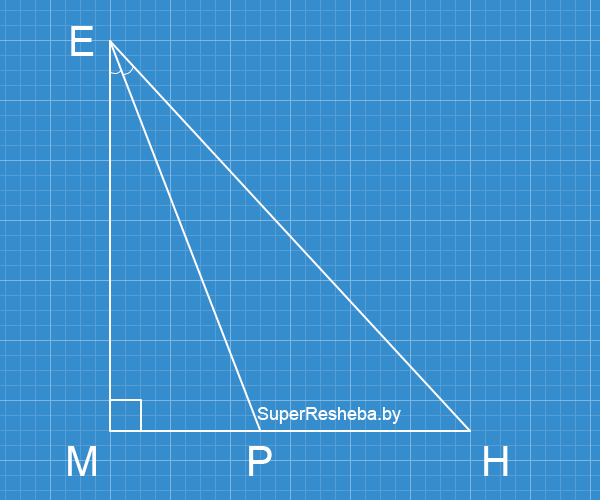
По теореме о биссектрисе треугольника $\dfrac{EM}{EH} = \dfrac{3}{5},$ тогда $EM = 3x;$ $EH = 5x.$ По теореме Пифагора $MH = 4x,$ тогда $\cos ∠EHM = \dfrac{MH}{EH} = \dfrac{4}{5}.$

Ответ: $\dfrac{4}{5}.$

Вариант 2

Биссектриса $KE$ прямоугольного треугольника $KPT$ $(∠P = 90°)$ делит катет $PT$ в отношении $5 : 13.$ Найдите косинус угла $KTP.$

Решение

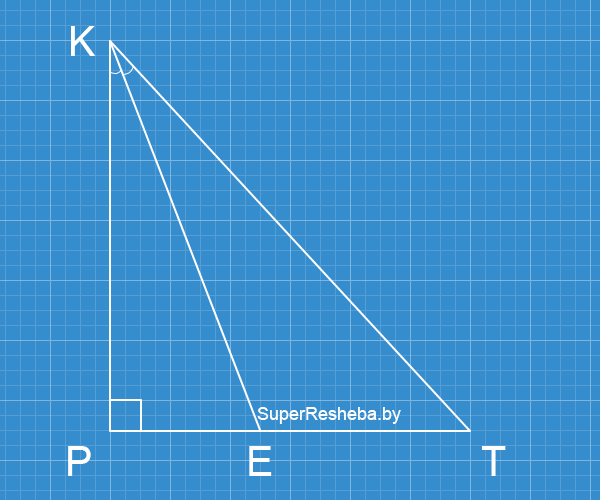
По теореме о биссектрисе треугольника $\dfrac{KP}{KT} = \dfrac{5}{13},$ тогда $KP = 5x;$ $KT = 13x.$ По теореме Пифагора $PT = 12x,$ тогда $\cos ∠KTP = \dfrac{PT}{KT} = \dfrac{12}{13}.$

Ответ: $\dfrac{12}{13}.$