Контр. 6. Рациональные выражения
1. Укажите рациональную дробь, имеющую смысл при любых значениях переменной $a$ [$b$]:
Вариант 1
| а) $\dfrac{a+9}{a};$ | в) $\dfrac{4a+3}{5+a};$ | д) $\dfrac{3a}{a^2+6}.$ |
| б) $\dfrac{24}{a-2};$ | г) $\dfrac{a+7}{a^2-9};$ |
Ответ: д) $\dfrac{3a}{a^2+6}.$
Вариант 2
| а) $\dfrac{b+4}{b^2-25};$ | в) $\dfrac{7}{b-3};$ | д) $\dfrac{b-5}{b}.$ |
| б) $\dfrac{4b}{b^2+8};$ | г) $\dfrac{5b-1}{3+b};$ |
Ответ: б) $\dfrac{4b}{b^2+8}.$
2.
Вариант 1
Укажите общий знаменатель дробей $\dfrac{3}{2b};$ $\dfrac{b-1}{9b^2c}$ и $\dfrac{1}{3c}:$
| а) $9b^2c;$ | б) $bc;$ | в) $18b^2c;$ | г) $3c;$ | д) $6b.$ |
Ответ: в) $18b^2c.$
Вариант 2
Укажите общий знаменатель дробей $\dfrac{5}{3a};$ $\dfrac{a-8}{8a^2d}$ и $\dfrac{1}{4d}:$
| а) $ad;$ | б) $a;$ | в) $8a^2d;$ | г) $4d;$ | д) $24a^2d.$ |
Ответ: д) $24a^2d.$
3. Выполните вычитание дробей:
Вариант 1
$\dfrac{2t-1}{3t}-\dfrac{1-t}{3t}$ $=\dfrac{2t-1-(1-t)}{3t}$ $=\dfrac{2t-1-1+t}{3t}$ $=\dfrac{3t-2}{3t}.$
Вариант 2
$\dfrac{4m-2}{5m}-\dfrac{2-m}{5m}$ $=\dfrac{4m-2-(2-m)}{5m}$ $=\dfrac{4m-2-2+m}{5m}$ $=\dfrac{5m-4}{5m}.$
4. Сократите дробь:
Вариант 1
$\dfrac{m^2-n^2}{m^2+n^2-2mn}$ $=\dfrac{(m-n)(m+n)}{(m-n)^2}$ $=\dfrac{m+n}{m-n}.$
Вариант 2
$\dfrac{c^2-a^2}{c^2+a^2-2ac}$ $=\dfrac{(c-a)(c+a)}{(c-a)^2}$ $=\dfrac{c-a}{c+a}.$
5. Выполните деление:
Вариант 1
$\dfrac{y^2-10y+25}{2y-10}:(5-y)^2$ $=\dfrac{y^2-10y+25}{(2y-10)(5-y)^2}$ $=\dfrac{y^2-10y+25}{(2y-10)(y^2-10y+25)}$ $=\dfrac{1}{2y-10}$ $=\dfrac{1}{2(y-5}.$
Вариант 2
$\dfrac{x^2-6x+9}{3x-9}:(3-x)^2$ $=\dfrac{x^2-6x+9}{(3x-9)(3-x)^2}$ $=\dfrac{x^2-6x+9}{(3x-9)(x^2-6x+9)}$ $=\dfrac{1}{3x-9}$ $=\dfrac{1}{3(x-3}.$
6. Выполните умножение:
Вариант 1
$\dfrac{3a+9b}{a-2b}·\dfrac{6b-3a}{9b^2+6ab+a^2}$ $=\dfrac{3(a+3b)}{a-2b}·\dfrac{3(2b-a)}{(3b+a)^2}$ $=\dfrac{9(2b-a)}{(a-2b)(3b+a)}$ $=-\dfrac{9(a-2b)}{(a-2b)(3b+a)}$ $=-\dfrac{9}{3b+a}.$
Вариант 2
$\dfrac{4a+2b}{a-3b}·\dfrac{6b-2a}{b^2+4ab+4a^2}$ $=\dfrac{2(2a+b)}{a-3b}·\dfrac{2(3b-2}{(b+2a)^2}$ $=\dfrac{2}{a-3b}·\dfrac{2(3b-2)}{b+2a}$ $=-\dfrac{4(2-3b)}{(a-3b)(b+2a)}$ $=-\dfrac{4}{b+2a}.$
7. Сократите дробь:

8. Упростите выражения:

9. Сократите дробь:
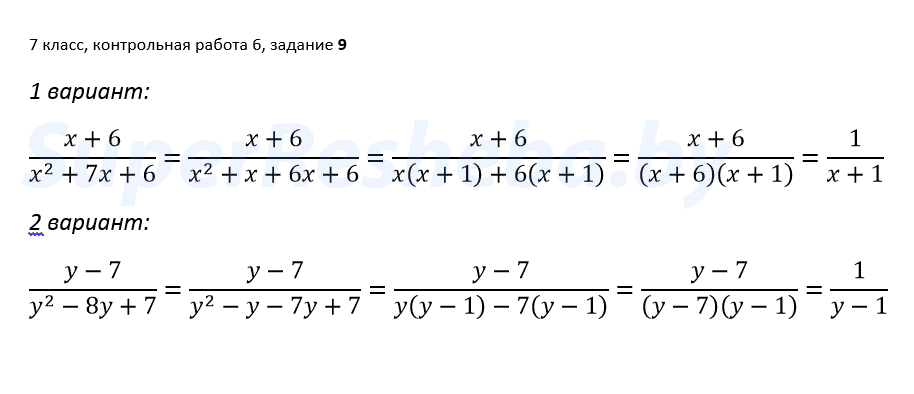
10. Сократите дробь:
