112. Точка P выбрана на ребре LL1 куба KLMNK1L1M1N1 (рис. 161). Сделайте такой рисунок в тетради и постройте точку пересечения с плоскостью M1N1M прямой q, проходящей через точку P и параллельной прямой NK1.

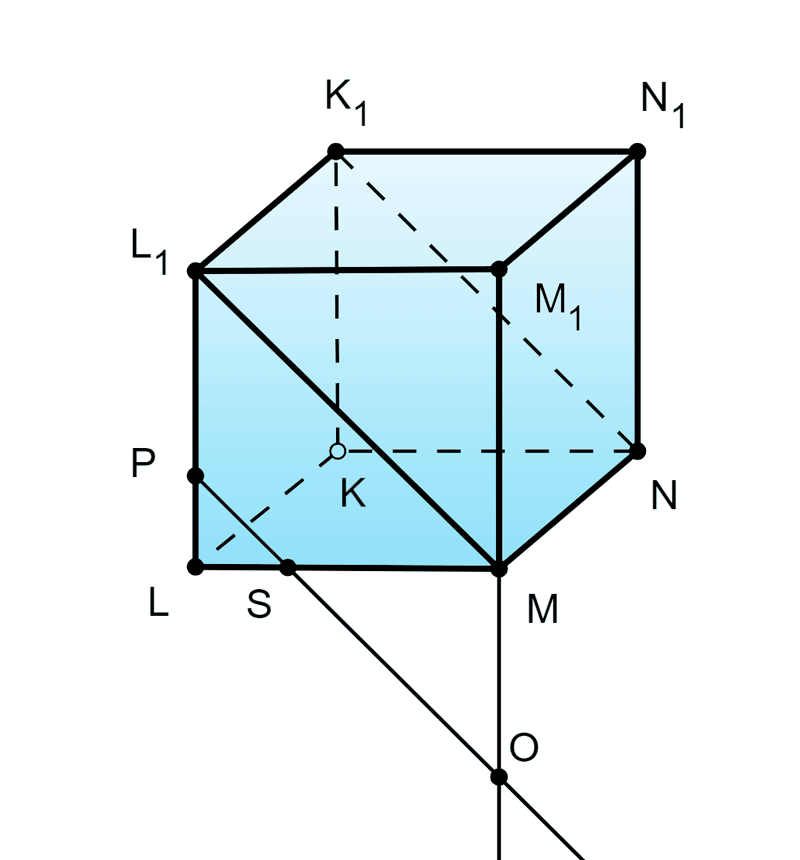
Дано: $KLMNK_1L_1M_1N_1$ — куб, $P\in LL_1,$ $P\in q, q\parallel NK_1.$

Построить: точку пересечения $q\cap (M_1N_1M).$

Решение:

1) Проведём диагональ $L_1M$ грани куба. Получим:

$L_1K_1NM$ — параллелограмм, т.к. $L_1K_1\parallel LK, LK\parallel MN \Rightarrow L_1K_1\parallel MN$ и $L_1K_1=MN$ как рёбра куба.

Через точку $P$ проведём прямую $q\parallel L_1M.$

2) $q\subset (LMM_1); MM_1\subset (LMM_1)\Rightarrow q\cap MM_1=O.$

3) $MM_1\subset (M_1N_1M) \Rightarrow q\cap (M_1N_1M)=O.$

$O$ — искомая точка.