111. Точки H, G, F, S — середины рёбер MN, ML, LK, KN треугольной пирамиды MKLN (рис. 160). Найдите периметр четырёхугольника HGFS, учитывая, что LN = 18 мм, MK = 22 мм.

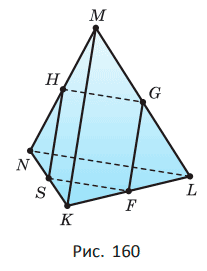
Дано: $MKLN$ — треугольная пирамида, $H$ — середина $MN,$ $G$ — середина $ML,$ $F$ — середина $LK,$ $S$ — середина $KN,$ $LN=18$ мм, $MK=22$ мм.

Найти: $P_{HGFS}.$

Решение:

1) $H$ — середина $MN$ и $S$ — середина $NK,$ значит $HS$ — средняя линия $\triangle MNK.$ По свойству средней линии $HS\parallel MK.$

$G$ — середина $ML$ и $F$ — середина $KL,$ значит $GF$ — средняя линия $\triangle MKL.$ По свойству средней линии $GF\parallel MK.$

$H$ — середина $MN$ и $G$ — середина $ML,$ значит $HG$ — средняя линия $\triangle MNL.$ По свойству средней линии $HG\parallel NL.$

$S$ — середина $NK$ и $F$ — середина $KL,$ значит $SF$ — средняя линия $△NKL.$ По свойству средней линии $SF\parallel NL.$

2) $HS\parallel MK$ и $GF\parallel MK,$ значит $HS\parallel GF.$

$HG\parallel NL$ и $SF\parallel NL,$ значит $HG\parallel SF.$

3) $HS\parallel GF$ и $HG\parallel SF,$ значит $HGFS$ — параллелограмм.

4) По свойству стороны параллелограмма $HG=SF=\dfrac{1}{2}NL=\dfrac{1}{2}\cdot 18=9\,(мм);$

$HS=GF=\dfrac{1}{2}MK=\dfrac{1}{2}\cdot 22\cdot 11\,(мм);$

$P_{HGFS}=(HG+HS)\cdot 2=(9+11)\cdot 2=40\,(мм).$

Ответ: 40 мм.