110. Точки M, N, U, V — соответственно середины рёбер AC, AD, BD, BC треугольной пирамиды ABCD (рис. 159). Найдите периметр четырёхугольника MNUV, учитывая, что AB = 20 см, CD = 30 см.

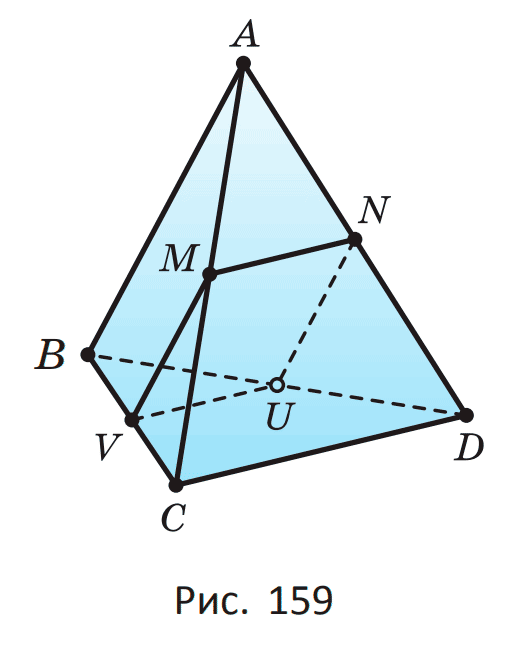
Дано: $ABCD$ — треугольная пирамида, $M$ — середина $AC,$ $N$ — середина $AD,$ $U$ — середина $DB,$ $V$ — середина $BC,$ $AB=20$ см, $CD=30$ см.

Найти: $P_{MNUV}.$

Решение:

1) $M$ — середина $AC$ и $V$ — середина $BC,$ значит $MV$ — средняя линия $\triangle ABC.$ Следовательно $MV\parallel AB.$

$N$ — середина $AD$ и $U$ — середина $BD,$ значит $NU$ — средняя линия $\triangle ABD.$ Следовательно $NU\parallel AB.$

$MV\parallel AB$ и $NU\parallel AB,$ значит $MV\parallel NU.$

$M$ — середина $AC$ и $N$ — середина $AD,$ значит $MN$ — средняя линия $\triangle ACD.$ Следовательно $MN\parallel CD.$

$V$ — середина $BC$ и $U$ — середина $BD,$ значит $VU$ — средняя линия $\triangle BCD.$ Следовательно $VU\parallel CD.$

2) $MN\parallel CD$ и $VU\parallel CD,$ значит $MN\parallel VU.$

$MV\parallel NU$ и $MN\parallel NU,$ значит $MNUV$ — параллелограмм.

3) $MV=NU=\dfrac{1}{2}AB=\dfrac{1}{2}\cdot 20=10\,(см);$

$MN=UV=\dfrac{1}{2}CD=\dfrac{1}{2}\cdot 30=15\,(см);$

$P_{MNKV}=\left( MN+NU\right) \cdot 2=(10+15)\cdot 2=50\,(см).$

Ответ: 50 см.