109. На отрезке AB, конец A которого принадлежит плоскости α, выбрана точка C, и через точки B и C проведены параллельные прямые, пересекающие плоскость α в точках B1 и C1 соответственно. Найдите отрезок CC1, учитывая, что:
а) точка C — середина отрезка AB и BB1 = 14 см;
б) AC : CB = 3 : 2 и BB1 = 50 см.
а)
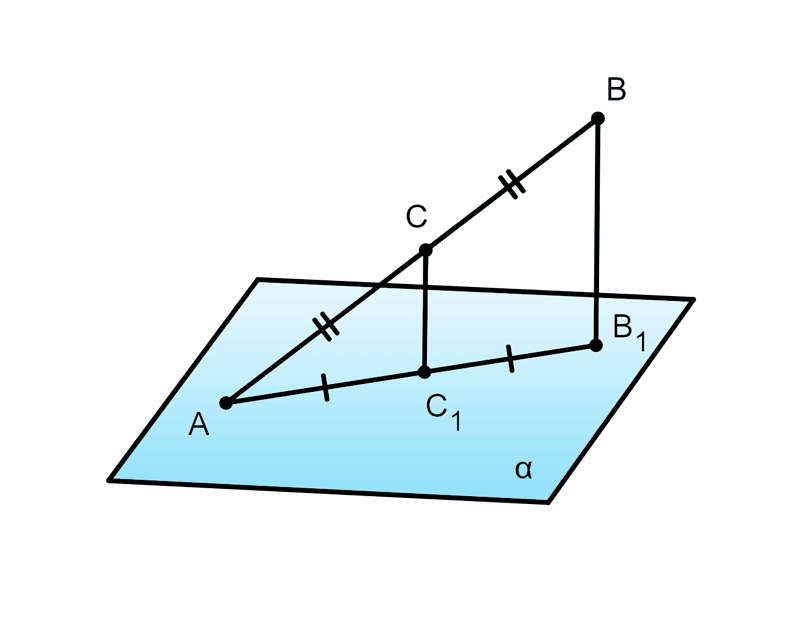
Дано: A∈α,C∈AB,CC1∩α=C1,BB1∩α=B1,CC1∥BB1,BB1=14 см, C — середина AB.
Найти: CC1.
Решение:
1) Параллельные прямые CC1 и BB1 задают плоскость (ABB1).
(ABB1)∩α=AB1.
Поэтому точки A,C1 и B1 лежат на одной прямой.
2) Т.к. C — середина AB и CC1∥BB1, то C1 — середина AB1. Значит, CC1 — средняя линия △ABB1. По свойству средней линии CC1=21BB1=21⋅14=7(см).
Ответ: 7 см.
б)
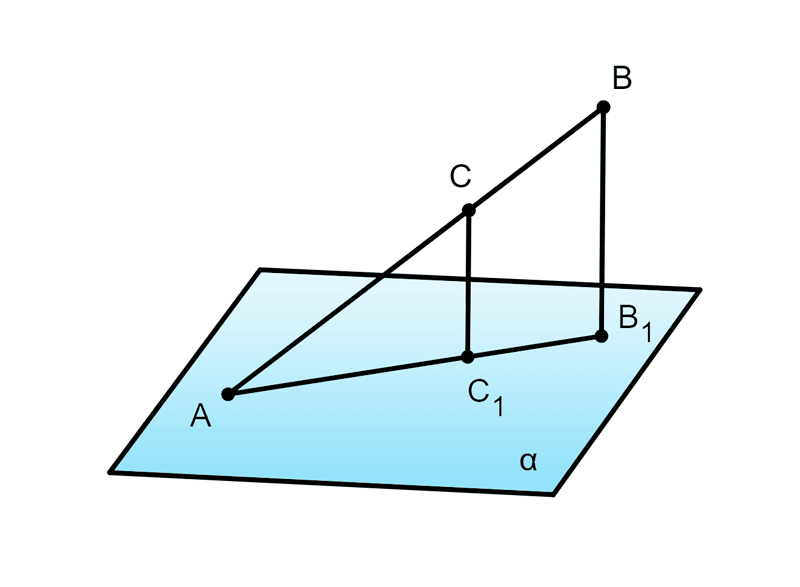
Дано: A∈α,C∈AB,CC1∩α=C1,BB1∩α=B1,CC1∥BB1,BB1=50см,AC:CB=3:2.
Найти: CC1.
Решение:
1) Рассмотрим △ACC1 и △ABB1.
∠A — общей,
∠AC1C=∠AB1B как соответственные при CC1∥BB1 и секущей AB1.
Следовательно △ACC1 подобен △ABB1 по двум углам.
2) ABAC=BB1CC1;
53=50CC1;
CC1=53⋅50=3⋅10=30(см).
Ответ: 30 см.

