108. Точка E является точкой отрезка TR, который не пересекает плоскость γ. Параллельные прямые, проведённые через точки T, R, E, пересекают плоскость γ в точках T1, R1, E1 соответственно. Докажите, что точки T1, R1, E1 лежат на одной прямой, и найдите отрезок EE1, учитывая, что TT1 = 27 см, RR1 = 15 см, TE : RE = 1 : 3.
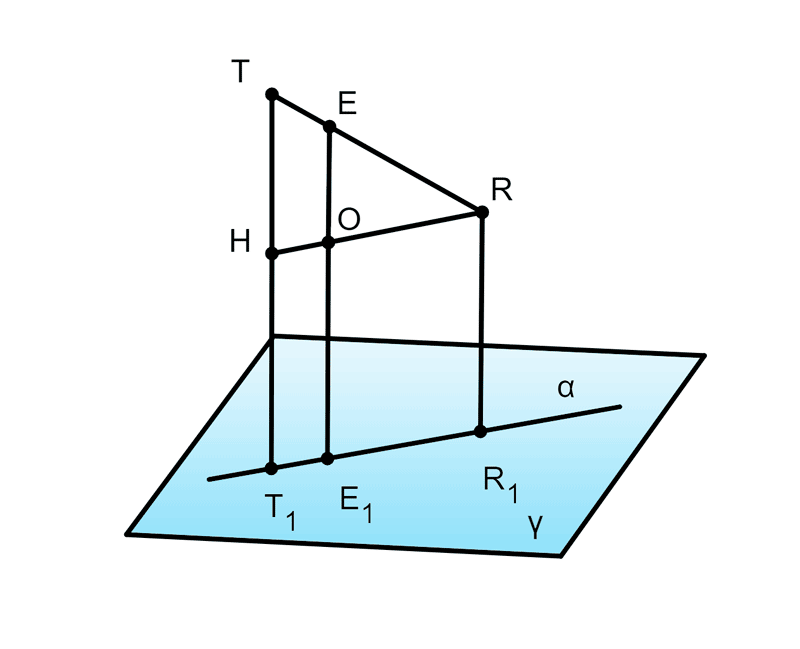
Дано: E∈TR,TT1∥EE1∥RR1,TT1∩γ=T1,EE1∩γ=E1,RR1∩γ=R1,TT1=27см,RR1=15см,TE:RE=1:3,a⊂γ.
Доказать: T1∈a,E1∈a,R1∈a.
Найти: EE1.
Решение:
1) Прямые TT1∥EE1∥RR1 задают плоскость (TRR1),(TRR1)∩γ=a. Следовательно T1,E1 и R1 лежат на прямой a.
2) Проведём прямую RH∥R1T1. Т.к. TT1∥RR1 и HT1∥RR1, то T1R1RH — параллелограмм по определению. По свойству сторон параллелограмма HT1=RR1 и HR=T1R1.
TH=TT1−HT1=TT1−RR1=27−15−12(см).
3) EE1∩HR=O.
Рассмотрим △ROE и △RHT.
∠R — общий,
∠EOR=∠THR как соответственные при TH∥EO и секущей HR.
Следовательно △ROE подобен △RHT по двум углам.
4) RTRE=THEO;
43=12EO;
EO=43⋅12=9(см).
5) EE1=EO+OE1=9+15=24(см), т.к. OE1R1R — параллелограмм и OE1=RR1.
Ответ: 24 см.
