107. Вершины M и N трапеции MNLK с основаниями NL и KM принадлежат плоскости γ, а две другие вершины не принадлежат ей. Найдите расстояние от точки M до точки пересечения прямой LK с плоскостью γ, учитывая, что MK = 16 см, MN = 9 см, NL = 12 см.

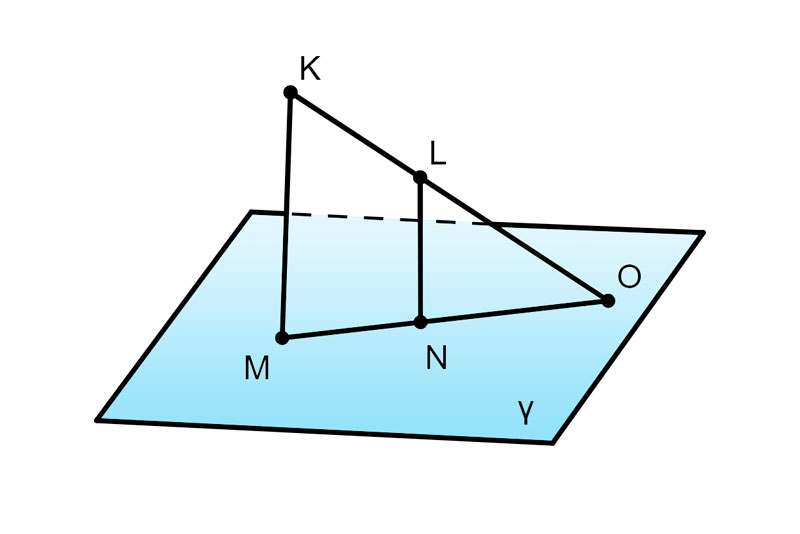
Дано: $MNLK$ — трапеция, $M\in γ, N\in γ, K\notin γ, L\notin γ, LN$ и $KM$ — основания трапеции, $LK\cap γ=O, MK=16$ см, $MN=9$ см, $NL=12$ см.

Найти: $MO$

Решение:

1) Так как $MNLK$ — трапеция с основаниями $LN$ и $KM,$ то $LN\parallel KM.$

2) Рассмотрим $\triangle LNO$ и $\triangle KMO:$

$\angle O$ — общий,

$\angle LNO = \angle KMO$ как соответственные при $KM\parallel LN$ и секущей $MO.$

Значит, $\triangle LNO$ подобен $\triangle KMO$ по двум углам.

3) $\dfrac{NO}{MO}=\dfrac{LN}{KM};$

$\dfrac{NO}{MN+NO}=\dfrac{12}{16};$

$\dfrac{NO}{9+NO}=\dfrac{3}{4};$

$\left( 9 + NO\right)\cdot 3=4\cdot NO;$

$27+3\cdot NO=4\cdot NO;$

$NO=27\,см.$

4) $MO=MN+NO=9+27=36\,(см).$

Ответ: $36$ см.