106. Точка P лежит на продолжении ребра NM параллелепипеда LKMNL1K1M1N1. Найдите расстояние от точки N до точки пересечения прямой M1P с плоскостью LL1N, учитывая, что MM1 = 24 м, NM = 12 м, PM = 18 м.

(см. задачу 2 стр. 56 учебника).

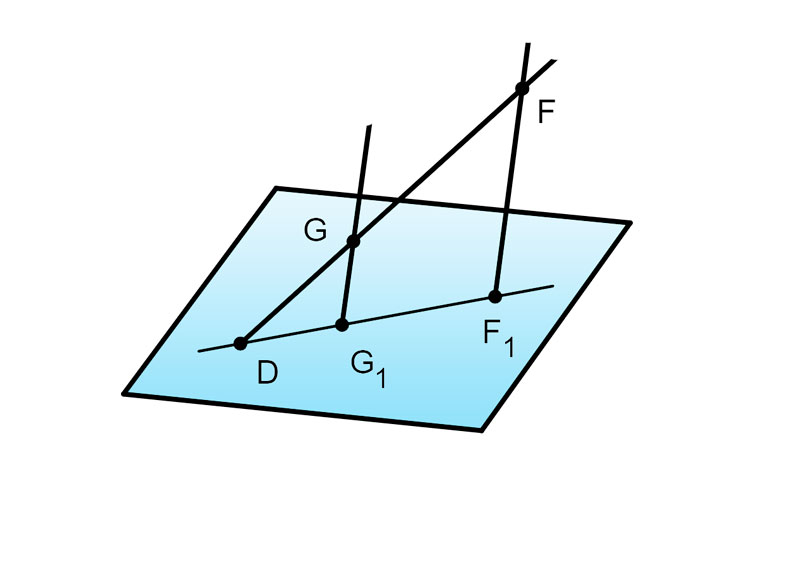
$DF$ — отрезок, $D\in \alpha, FF_1 \parallel GG_1, FF_1=23$ см.

$DG:GF=3:5,$ значит

$DG:DF=3:8,$

$\triangle DGG_1$ подобен $\triangle DFF_1, k=\dfrac{DG}{DF}=\dfrac{3}{8}.$

$GG_1=FF_1\cdot k=32\cdot \dfrac{3}{8}=12$ см.

Ответ: 12 см.