38. Основанием прямой призмы является прямоугольный треугольник, один из катетов которого равен 5 см. Найдите объем призмы, учитывая, что радиус окружности, описанной около основания призмы, равен 6,5 см, а высота призмы — 10 см.

Рассмотрим прямую треугольную призму ABCA1B1C1,ABCA_1B_1C_1, в основании которой лежит ΔBAC,\Delta BAC, в котором ∠BAC=90°,AB=5 см,\angle BAC=90°, AB=5\,см, а боковое ребро AA1=h=10 см.AA_1=h=10\,см. Опишем окружность около основания призмы, по условию её радиус R=6.5 см:R=6.5\,см:

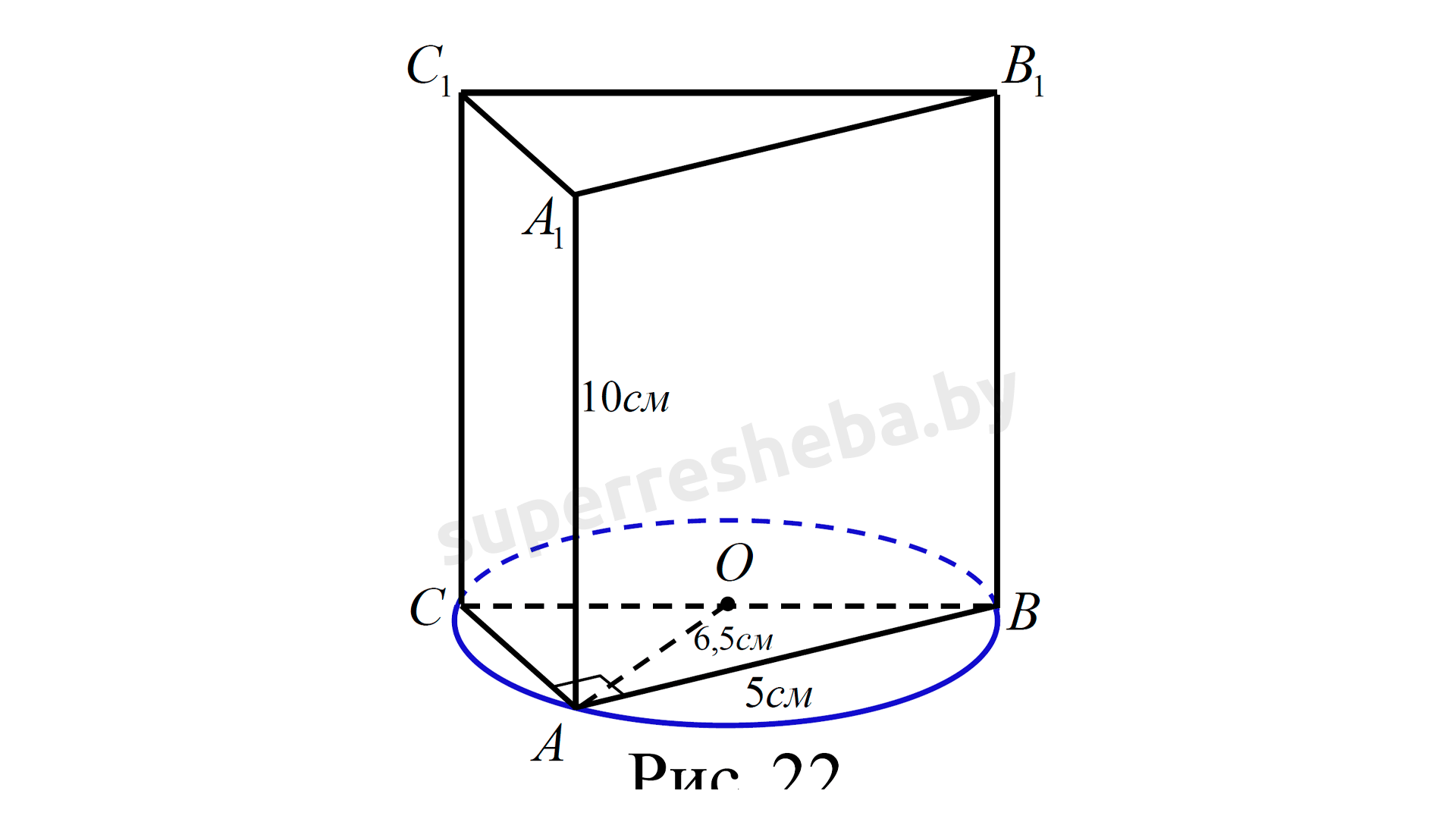
Учитывая, что центр окружности описанной около прямоугольного треугольника лежит на средине гипотенузы, получим:

CB=2R=2⋅6.5=13 (см).CB=2R=2\cdot 6.5=13\,(см).

С прямоугольного ΔBAC,\Delta BAC, применяя теорему Пифагора, найдём катет AC:AC:

AC=CB2−AB2=132−52=144=12 (см).AC=\sqrt{CB^2-AB^2}=\sqrt{13^2-5^2}=\sqrt{144}=12\,(см).

Объём прямой призмы, вычисляется по формуле:

V=Sосн⋅AA1=12⋅AC⋅AB⋅AA1=12⋅12⋅5⋅10=300 (см3).V=S_{осн}\cdot AA_1=\dfrac{1}{2}\cdot AC\cdot AB\cdot AA_1=\dfrac{1}{2}\cdot 12\cdot 5\cdot 10=300\,(см^3).

Ответ: 300 см3.300\,см^3.