34. Найдите объем прямоугольного параллелепипеда, стороны основания которого равны a и b, а высота — h, учитывая, что:
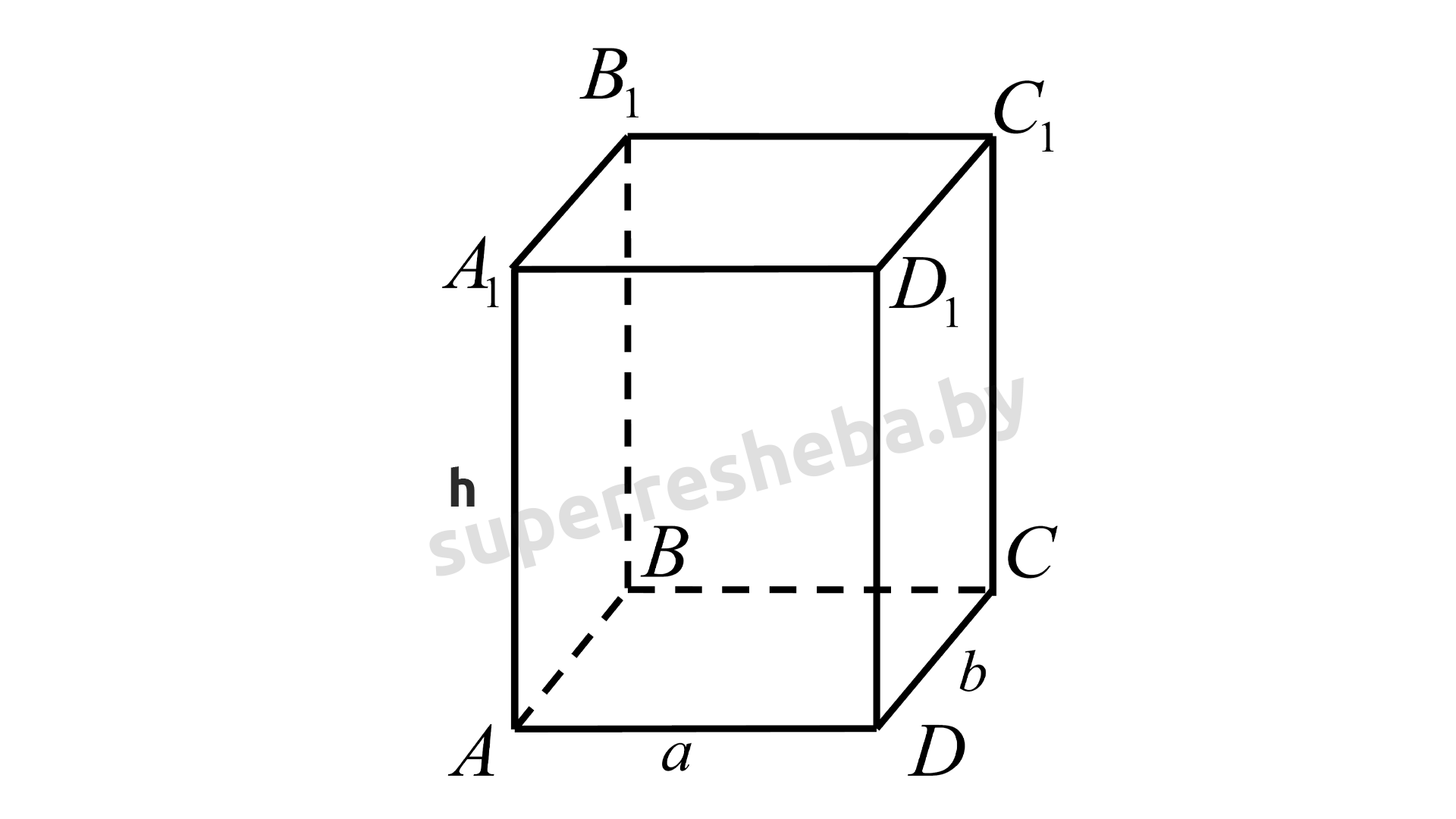
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1, объём которого вычисляется по формуле:
V=abh.
Тогда:
а) V=abh=22⋅24⋅30=15840;
б) V=abh=92⋅35⋅3010=8100;
в) V=abh=72⋅203⋅52=748803;
г) V=abh=331⋅5⋅0.96=310⋅5⋅2524=2⋅5⋅58=3.25.
Ответ: а) 15840; б) 8100; в) 748803; г) 3.25.
