33. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. Через противолежащий ему катет и противолежащую этому катету вершину основания проведено сечение, составляющее угол β с плоскостью основания. Определите, какую часть от площади боковой поверхности призмы составляет площадь сечения.

Рассмотрим прямую треугольную призму ABCA1B1C1,ABCA_1B_1C_1, в основании которой лежит ΔACB,\Delta ACB, в котором ∠ACB=90°,∠ABC=φ.\angle ACB=90°, \angle ABC=\varphi.

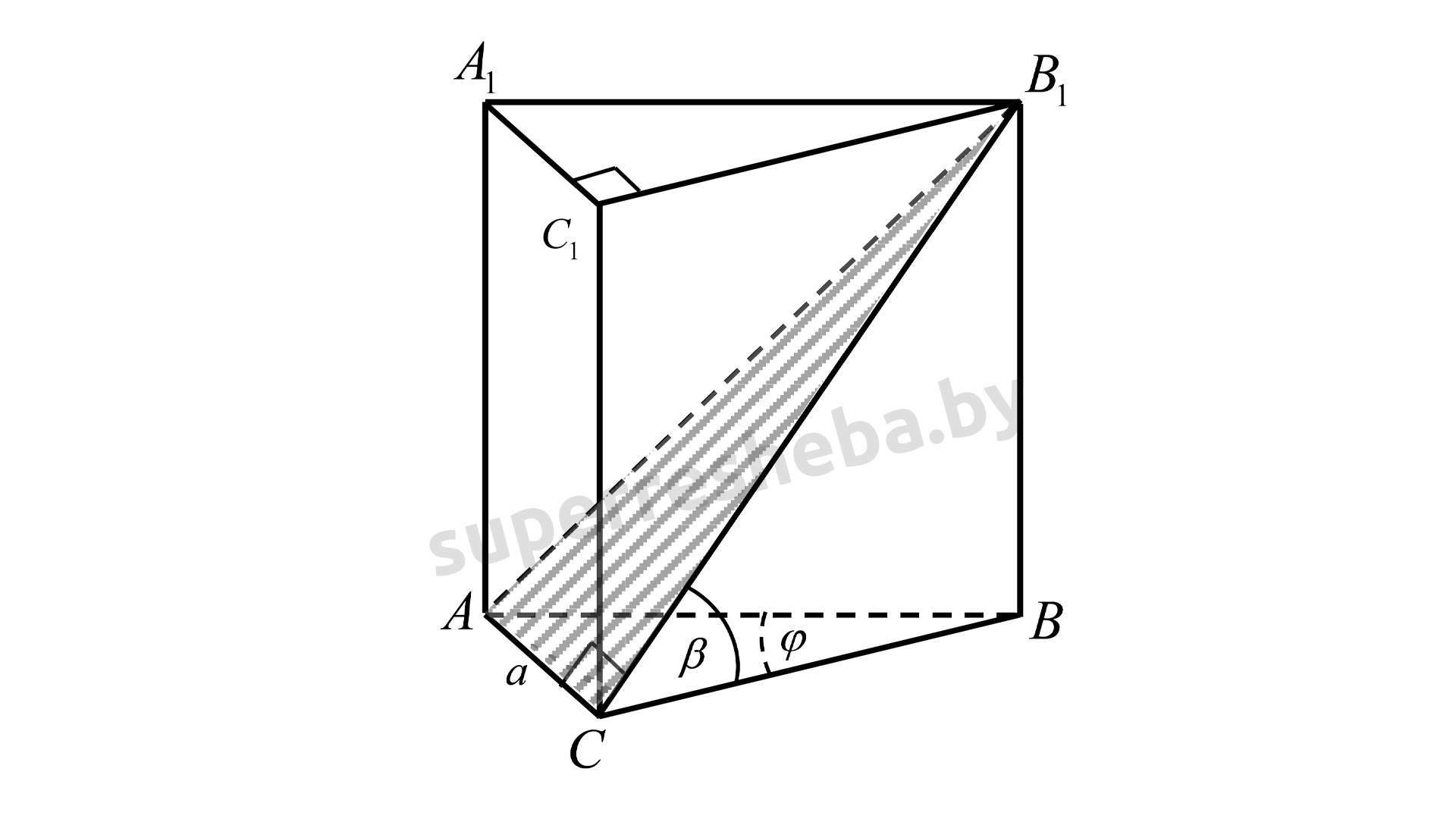
Построим сечение ACB1,ACB_1, которое проходит через катет AC,AC, противоположный ∠ABC,\angle ABC, и противолежащую вершину B1.B_1. Поскольку BCBC — проекция B1CB_1C на плоскость основания и BC⊥AC,BC\perp AC, то по обратной теореме о трёх перпендикулярах B2C⊥AC,B_2C\perp AC, а по определению угла между плоскостями ∠B1CB\angle B_1CB — линейный угол между плоскостью сечения и плоскостью основания. По условию задачи  ∠B1CB=β.\angle B_1CB=\beta.

Пусть AC=a.AC=a. Тогда с прямоугольного ΔABC,\Delta ABC, применяя соотношения между его сторонами, получаем:

BC=ACtg⁡φ=atg⁡φ;BC=\dfrac{AC}{\tg\varphi}=\dfrac{a}{\tg\varphi};

AB=ACsin⁡φ=asin⁡φ.AB=\dfrac{AC}{\sin\varphi}=\dfrac{a}{\sin\varphi}.

C прямоугольного ΔCBB1,\Delta CBB_1, применяя соотношения между его сторонами, получаем:

BB1=BC⋅tg⁡β=a⋅tg⁡βtg⁡φ;BB_1=BC\cdot \tg\beta=\dfrac{a\cdot \tg\beta}{\tg\varphi};

CB1=BCcos⁡β=atg⁡φ⋅cos⁡β.CB_1=\dfrac{BC}{\cos\beta}=\dfrac{a}{\tg\varphi\cdot \cos\beta}.

Вычисляем площадь сечения:

SACB1=12⋅AC⋅CB1=12⋅a⋅atg⁡φ⋅cos⁡β=a22tg⁡φ⋅cos⁡β.S_{ACB_1}=\dfrac{1}{2}\cdot AC\cdot CB_1=\dfrac{1}{2}\cdot a\cdot \dfrac{a}{\tg\varphi\cdot \cos\beta}=\dfrac{a^2}{2\tg\varphi\cdot \cos\beta}.

Боковая поверхность прямой призмы равна произведению периметра основания на боковое ребро:

Sбок=(AC+BC+AB)⋅BB1;S_{бок}=(AC+BC+AB)\cdot BB_1;

Sбок=(a+atg⁡φ+asin⁡φ)a⋅tg⁡βtg⁡φ=(1+1tg⁡φ+1sin⁡φ)a2⋅tg⁡βtg⁡φ.S_{бок}=\left( a+\dfrac{a}{\tg\varphi}+\dfrac{a}{\sin\varphi}\right)\dfrac{a\cdot \tg\beta}{\tg\varphi}=\left(1+\dfrac{1}{\tg\varphi}+\dfrac{1}{\sin\varphi}\right)\dfrac{a^2\cdot \tg\beta}{\tg\varphi}.

Определяем, какую часть от площади боковой поверхности призмы составляет площадь сечения:

SACB1Sбок=a22tg⁡φ⋅cos⁡β(1+1tg⁡φ+1sin⁡φ)2a2⋅tg⁡βtg⁡φ=12⋅cos⁡β(1+ctg⁡φ+1sin⁡φ)tg⁡β=1ssin⁡β⋅(1+ctg⁡φ+1sin⁡φ).\dfrac{S_{ACB_1}}{S_{бок}}=\dfrac{\dfrac{a^2}{2\tg\varphi\cdot \cos\beta}}{\left( 1+\dfrac{1}{\tg\varphi}+\dfrac{1}{\sin\varphi}\right)^2\dfrac{a^2\cdot \tg\beta}{\tg\varphi}}=\dfrac{\dfrac{1}{2\cdot \cos\beta}}{\left(1+\ctg\varphi+\dfrac{1}{\sin\varphi}\right) \tg\beta}=\dfrac{1}{s\sin\beta\cdot \left(1+\ctg\varphi +\dfrac{1}{\sin\varphi}\right)}.

Ответ: 1ssin⁡β⋅(1+ctg⁡φ+1sin⁡φ).\dfrac{1}{s\sin\beta\cdot \left(1+\ctg\varphi +\dfrac{1}{\sin\varphi}\right)}.