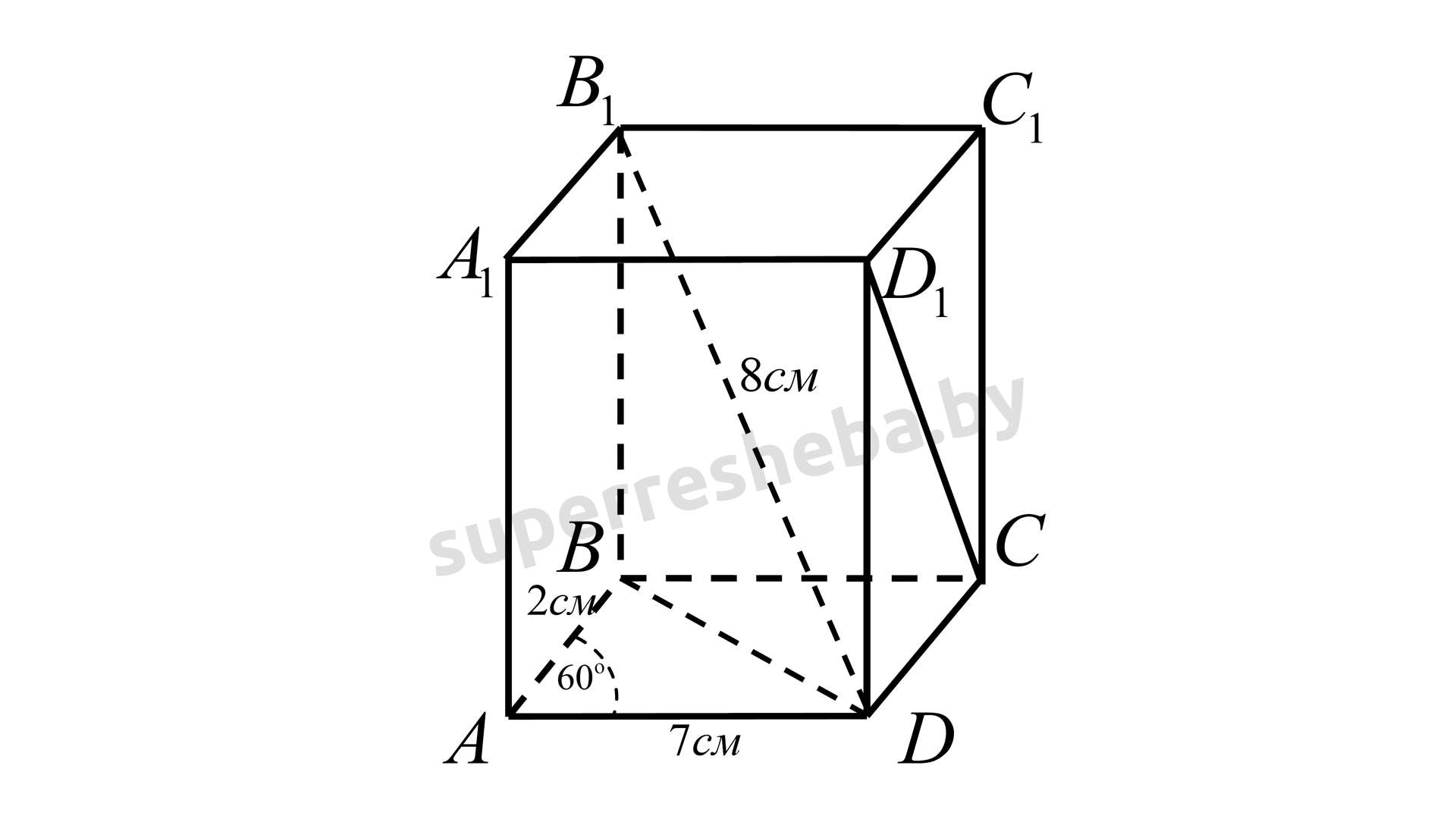
29. Найдите боковую поверхность прямого параллелепипеда, учитывая, что стороны его основания равны 2 см и 7 см, меньшая диагональ параллелепипеда — 8 см и один из углов основания — 60°.

Рассмотрим прямой параллелепипед ABCDA1B1C1D1.ABCDA_1B_1C_1D_1. С ΔABD\Delta ABD по теореме косинусов найдём квадрат стороны BD:BD:

BD2=AB2+AD2−2AB⋅AD⋅cos⁡∠BAD;BD^2=AB^2+AD^2-2AB\cdot AD\cdot \cos\angle BAD;

BD2=22+72−2⋅2⋅7⋅cos⁡60°=39 (см2).BD^2=2^2+7^2-2\cdot 2\cdot 7\cdot \cos 60°=39\,(см^2).

С прямоугольного ΔB1BD,\Delta B_1BD, учитывая теорему Пифагора, найдём ВВ1ВВ_1 боковое ребро параллелепипеда:

BB1=B1D2−BD2=82−39=5 (см).BB_1=\sqrt{B_1D^2-BD^2}=\sqrt{8^2-39}=5\,(см).

Боковая поверхность прямого параллелепипеда равна произведению периметра основания на боковое ребро:

Sбок=2(AB+AD)⋅BB1=2⋅(2+7)⋅5=90 (см2).S_{бок}=2(AB+AD)\cdot BB_1=2\cdot (2+7)\cdot 5=90\,(см^2).

Найдём объём заданного прямого параллелепипеда по формуле:

V=Sосн⋅BB1=AB⋅AD⋅sin⁡∠BAD⋅BB1;V=S_{осн}\cdot BB_1=AB\cdot AD\cdot\sin \angle BAD\cdot BB_1;

V=2⋅7⋅sin⁡60°⋅5=353 (см3).V=2\cdot 7\cdot \sin 60°\cdot 5=35\sqrt{3}\,(см^3).

Ответ: 90 см2,353 см3.90\, см^2, 35\sqrt{3}\,см^3.