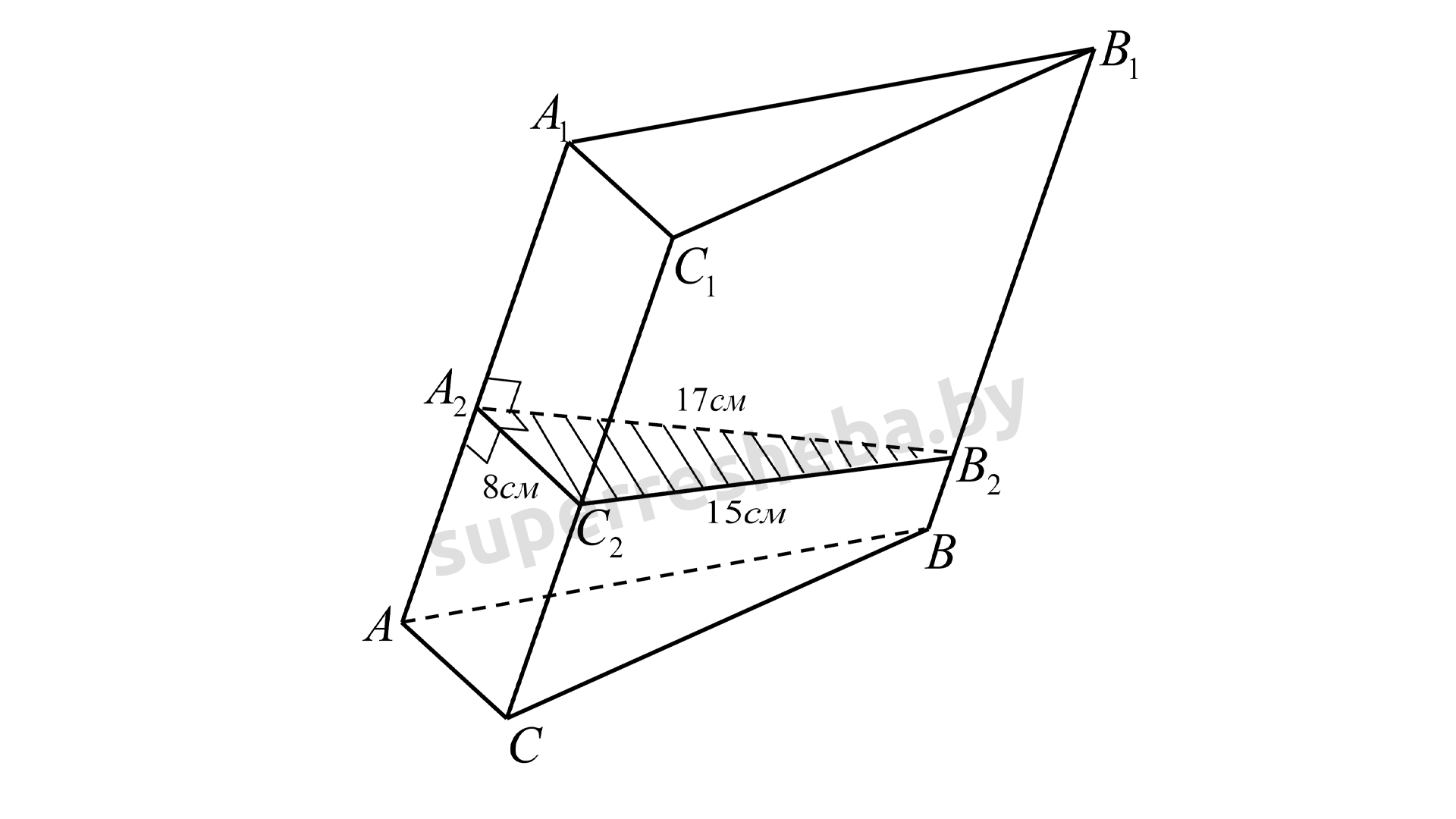
27. В наклонной треугольной призме расстояния между боковыми ребрами равны 15 см, 17 см, 8 см. Найдите боковое ребро призмы, учитывая, что ее боковая поверхность равновелика перпендикулярному сечению.
Рассмотрим наклонную треугольную призму A B C A 1 B 1 C 1 . ABCA_1B_1C_1. A BC A 1 B 1 C 1 . Построим сечение Δ A 2 B 2 C 2 , \Delta A_2B_2C_2, Δ A 2 B 2 C 2 , перпендикулярное ребру A A 1 . AA_1. A A 1 .
Найдём площадь сечения Δ A 2 B 2 C 2 \Delta A_2B_2C_2 Δ A 2 B 2 C 2 по формуле Герона:
S A 2 B 2 C 2 = p ( p − a ) ( p − b ) ( p − c ) ; S_{A_2B_2C_2}=\sqrt{p(p-a)(p-b)(p-c)}; S A 2 B 2 C 2 = p ( p − a ) ( p − b ) ( p − c ) ;
a = A 2 B 2 = 17 см ; a=A_2B_2=17\,см; a = A 2 B 2 = 17 см ;
b = A 2 C 2 = 8 см ; b=A_2C_2=8\,см; b = A 2 C 2 = 8 см ;
c = B 2 C 2 = 15 см ; c=B_2C_2=15\,см; c = B 2 C 2 = 15 см ;
p = A 2 B 2 + A 2 C 2 + B 2 C 2 2 = 17 + 8 + 15 2 = 20 ( см ) ; p=\dfrac{A_2B_2+A_2C_2+B_2C_2}{2}=\dfrac{17+8+15}{2}=20\,(см); p = 2 A 2 B 2 + A 2 C 2 + B 2 C 2 = 2 17 + 8 + 15 = 20 ( см ) ;
S A 2 B 2 C 2 = 20 ⋅ ( 20 − 17 ) ⋅ ( 20 − 8 ) ⋅ ( 20 − 15 ) = 20 ⋅ 3 ⋅ 12 ⋅ 5 = 200 ⋅ 36 = 60 ( с м 2 ) . S_{A_2B_2C_2}=\sqrt{20\cdot (20-17)\cdot (20-8)\cdot(20-15)}=\sqrt{20\cdot 3\cdot 12\cdot 5}=\sqrt{200\cdot 36}=60\,(см^2). S A 2 B 2 C 2 = 20 ⋅ ( 20 − 17 ) ⋅ ( 20 − 8 ) ⋅ ( 20 − 15 ) = 20 ⋅ 3 ⋅ 12 ⋅ 5 = 200 ⋅ 36 = 60 ( с м 2 ) .
S бок = S A 2 B 2 C 2 = 60 с м 2 . S_{бок}=S_{A_2B_2C_2}=60\,см^2. S бок = S A 2 B 2 C 2 = 60 с м 2 .
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения призмы на боковое ребро:
S бок = 2 p ⋅ A A 1 ; S_{бок}=2p\cdot AA_1; S бок = 2 p ⋅ A A 1 ;
A A 1 = S бок 2 p = 60 2 ⋅ 20 = 1.5 см . AA_1=\dfrac{S_{бок}}{2p}=\dfrac{60}{2\cdot 20}=1.5\,см. A A 1 = 2 p S бок = 2 ⋅ 20 60 = 1.5 см .
Ответ: 1.5 см . 1.5\,см. 1.5 см .