23. По стороне основания a и боковому ребру l найдите полную поверхность правильной призмы, основанием которой является: а) треугольник; б) четырехугольник; в) шестиугольник.
Площадь полной поверхности правильной призмы, вычисляется по формуле:
а) Если в основании правильной призмы лежит треугольник, то площадь основания вычисляем по формуле площади правильного треугольника со стороной
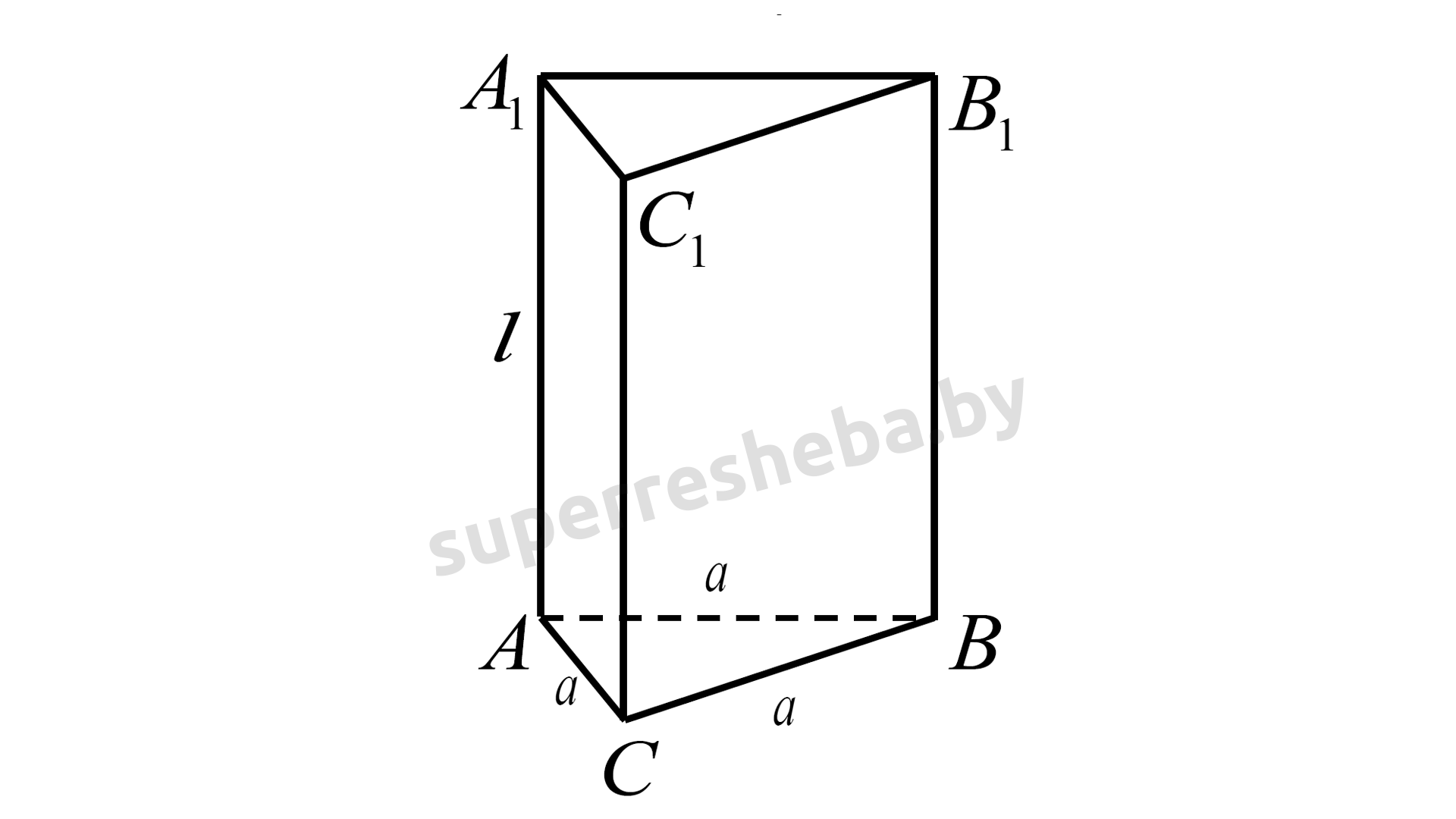
Площадь боковой поверхности правильной треугольной призмы вычисляется по формуле:
Тогда:
б) Если в основании правильной призмы лежит четырехугольник , то площадь основания вычисляем по формуле площади квадрата со стороной
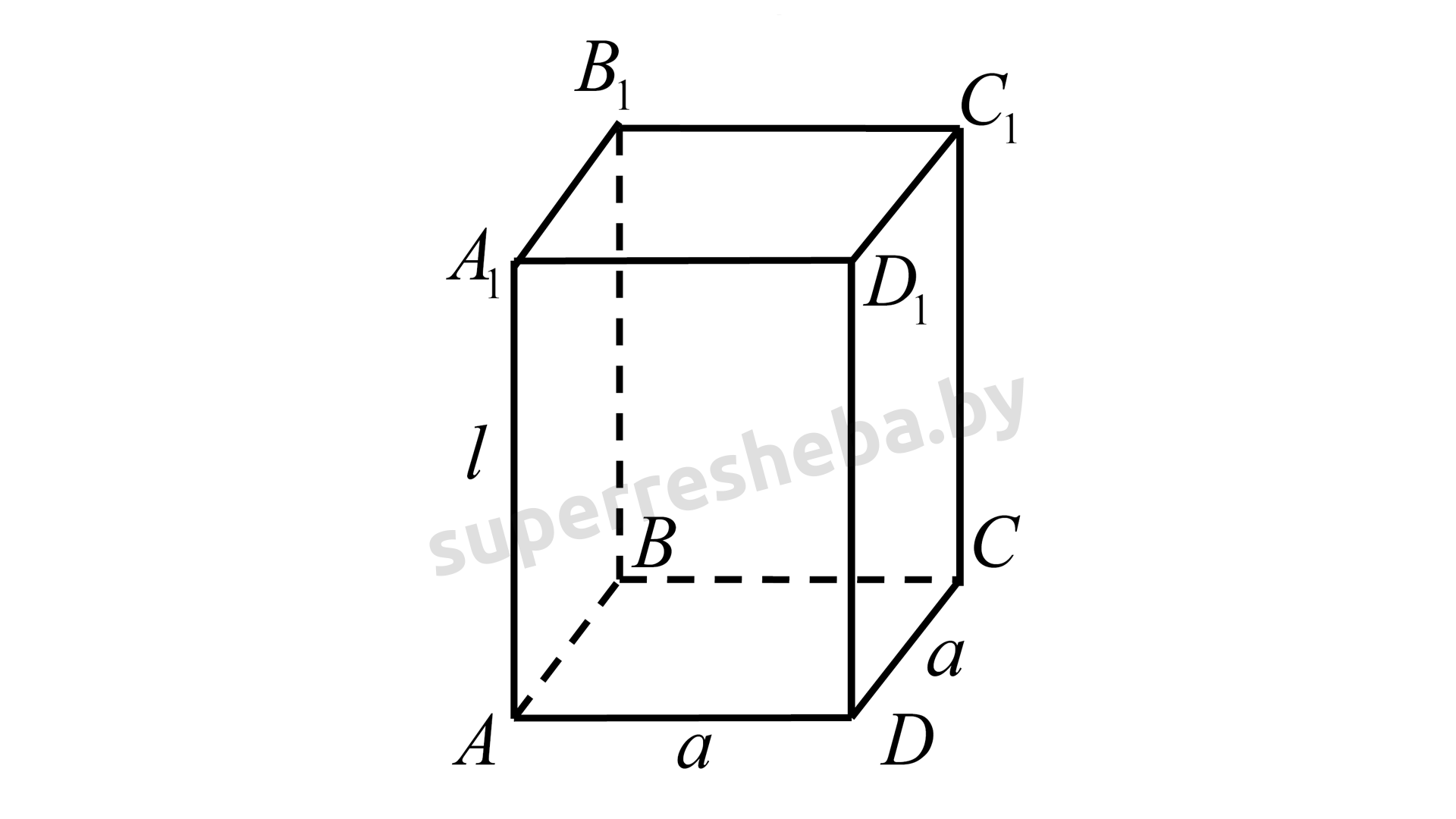
Площадь боковой поверхности правильной четырёхугольной призмы вычисляется по формуле:
Тогда:
в) Если в основании правильной призмы лежит шестиугольник, то площадь основания вычисляем по формуле правильного шестиугольника со стороной
Площадь боковой поверхности правильной шестиугольной призмы вычисляется по формуле:
Тогда:
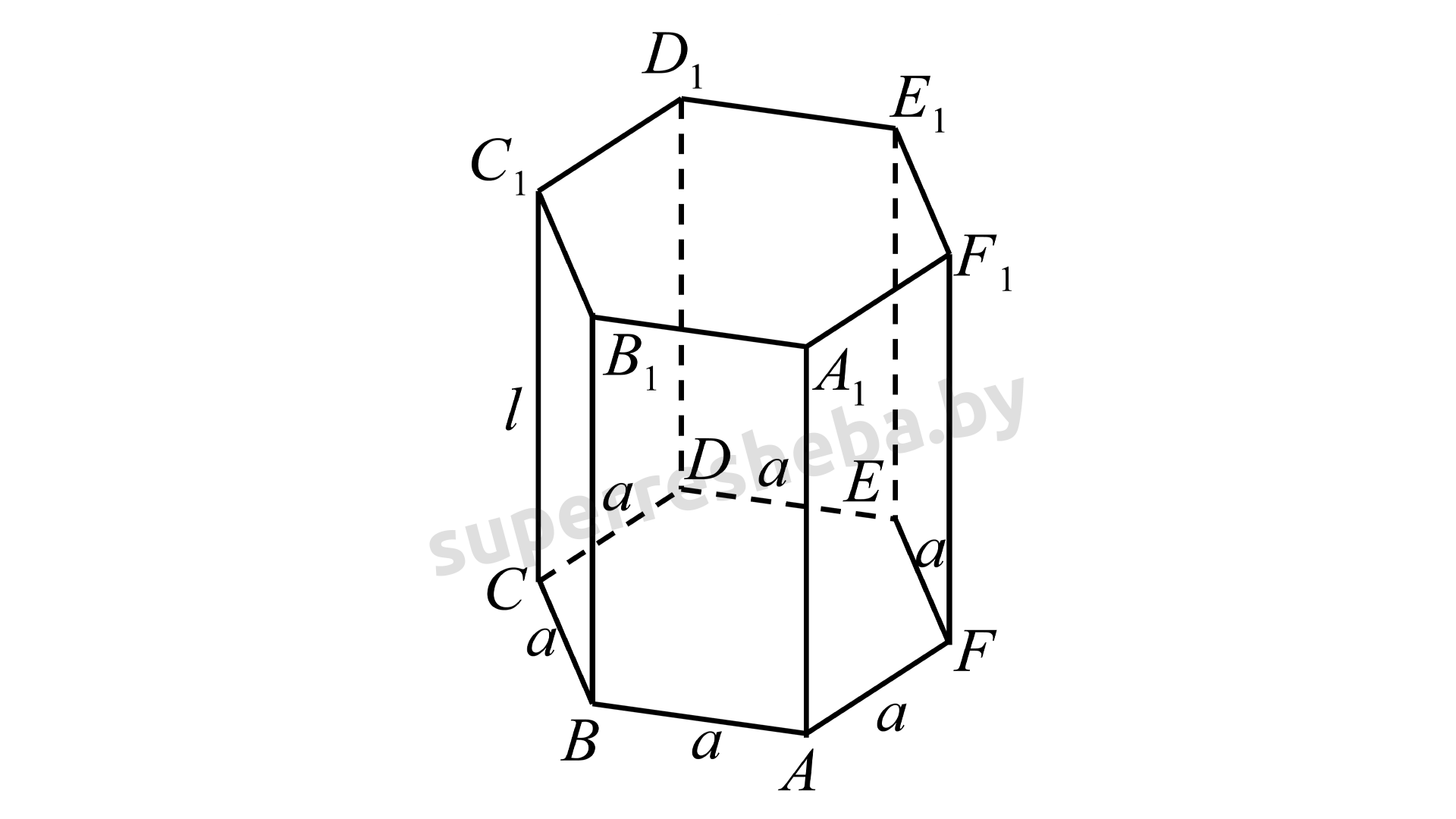
Ответ: а) б) в)