22. В прямой треугольной призме с боковой поверхностью 48 см2 все ребра равны. Найдите высоту призмы.
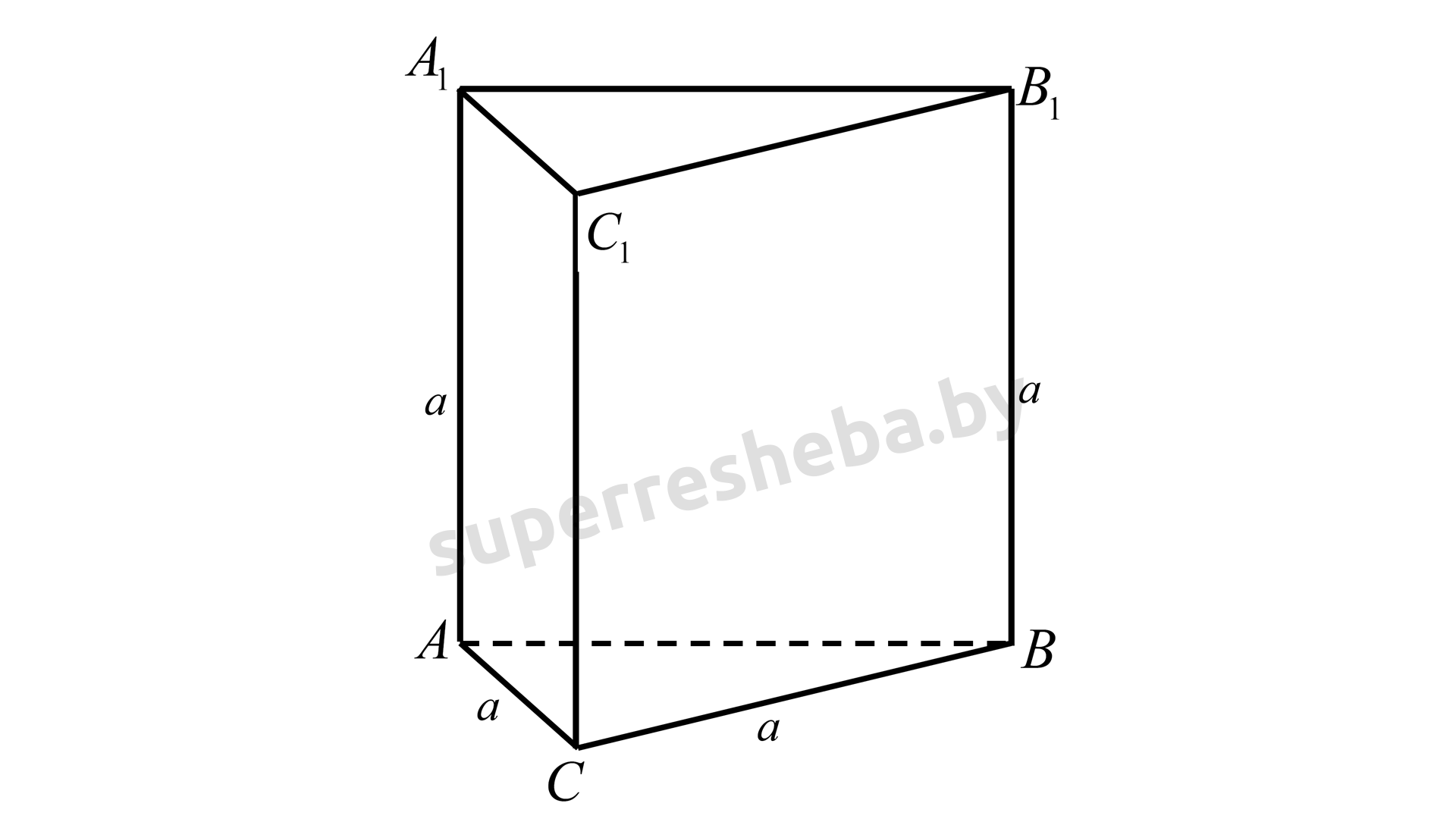
Рассмотрим прямую треугольную призму ABCA1B1C1. Площадь боковой поверхности прямой треугольной призмы вычисляется по формуле:
Sб=(AB+BC+AC)⋅AA1.
По условию задачи AB=BC=AC=AA1, тогда:
Sб=3⋅AA1⋅AA1;
Sб=3AA12;
AA1=3Sб=348=16=4(см).
Ответ:AA1=4см.
