21. Найдите площадь поверхности прямоугольного параллелепипеда, учитывая, что его измерения равны 8 см, 10 см, 11 см.

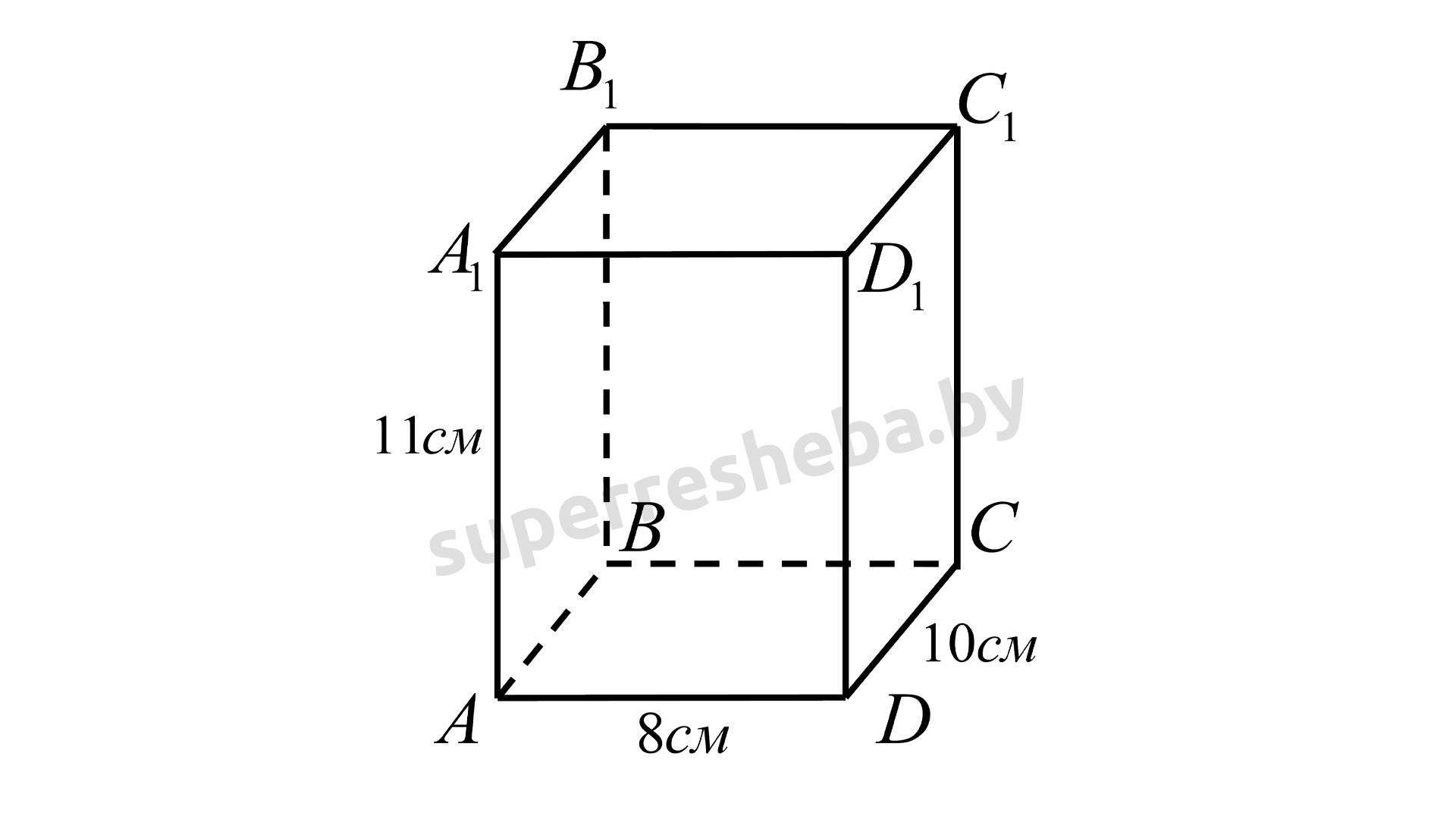
Рассмотрим прямоугольный параллелепипед $ABCDA_1B_1C_1D_1.$ Площадь поверхности прямоугольного параллелепипеда вычисляется по формуле:

$S_{пол}=2S_{осн}+S_б,$

где $S_{осн}$ — площадь основания, $S_б$ — площадь боковой поверхности прямоугольного параллелепипеда.

Вычислим площадь основания:

$S_{осн}=AB\cdot AD=8\cdot 10=80\,(см^2).$

Вычислим площадь боковой поверхности:

$S_б=2(AB+AD)\cdot AA_1;$

$S_б=2\cdot (8+10)\cdot 11=396\,(см^2).$

Тогда площадь полной поверхности будет равна:

$S_{пол}=2\cdot 80+396=556\,(см^2).$

Ответ: $S_{пол}=556\,см^2.$