17. Боковое ребро AA1 призмы, основанием которой является правильный треугольник ABC, образует равные углы со сторонами основания AC и AB. Докажите, что: а) стороны BC и AA1 перпендикулярны; б) четырехугольник CC1B1B является прямоугольником.

Доказательство:

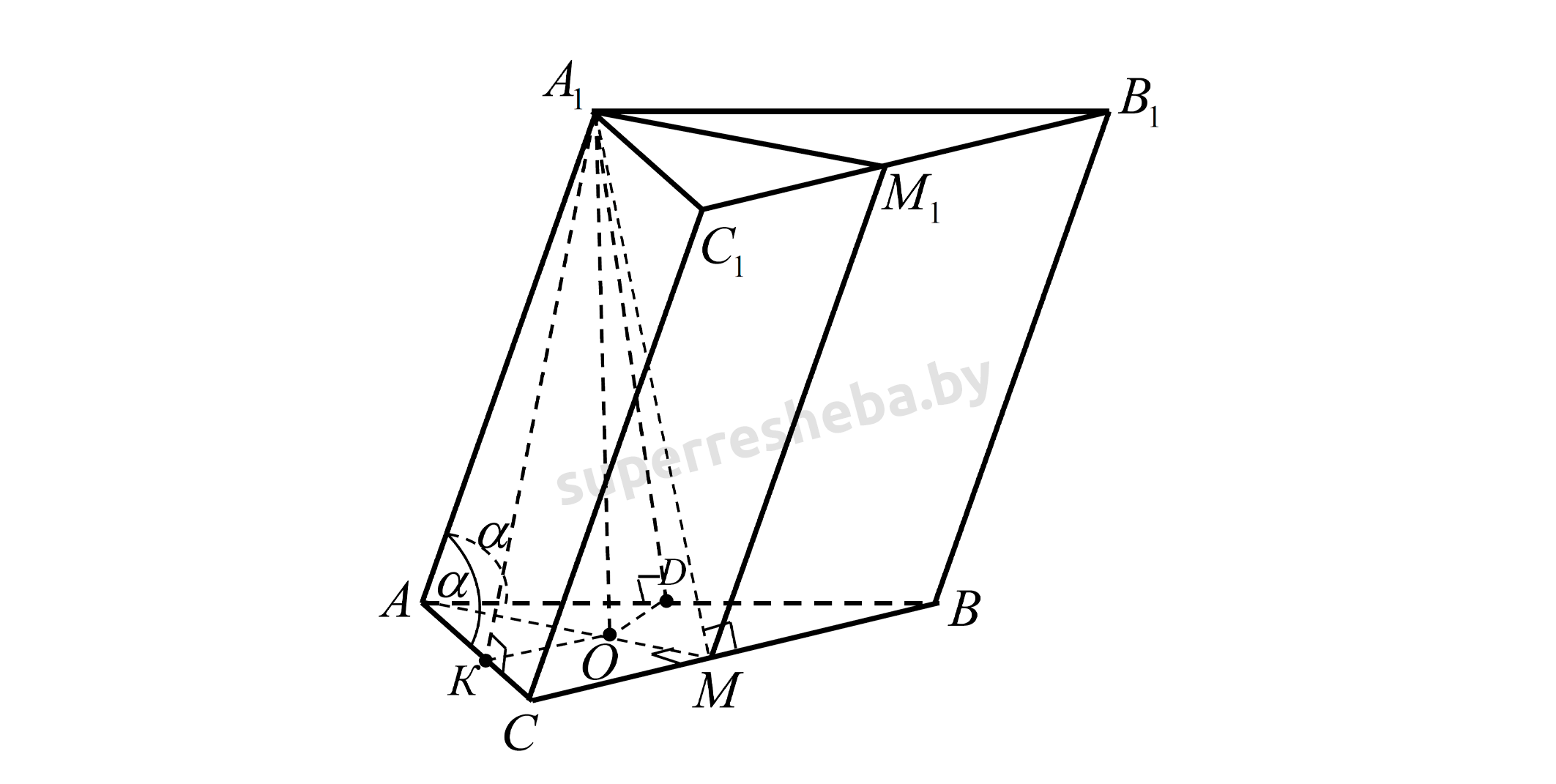
Рассмотрим треугольную призму ABCA1B1C1,ABCA_1B_1C_1, в основании которой лежит равносторонний ΔABC.\Delta ABC. По условию ∠A1AB=∠A1AC=α.\angle A_1AB=\angle A_1AC=\alpha.

а) Докажем, что AC⊥AA1.AC\perp AA_1. Построим A1K⊥ACA_1K\perp AC и A1D⊥AB.A_1D\perp AB. Тогда ΔA1DA=ΔA1KA\Delta A_1DA=\Delta A_1KA (как прямоугольные треугольники, у которых равны гипотенузы и острый угол). Следовательно, A1D=A1K.A_1D=A_1K.

Построим высоту призмы A1O.A_1O. Тогда ΔA1OK=ΔA1OD\Delta A_1OK=\Delta A_1OD (как прямоугольные треугольники, у которых равны гипотенузы и один катет). Следовательно, OD=OK.OD=OK.

Поскольку A1D⊥ABA_1D\perp AB и ODOD — проекция A1DA_1D на плоскость основания, то по теореме о трёх перпендикулярах OD⊥AB.OD\perp AB. Аналогично OK⊥AC.OK\perp AC. Тогда ΔA1DO=ΔA1KO\Delta A_1DO=\Delta A_1KO (как прямоугольные треугольники, у которых равны гипотенузы и один катет). Следовательно, ∠KAO=∠DAA\angle KAO=\angle DAA и точка OO лежит на биссектрисе ∠CAB.\angle CAB. По теореме о медиане равнобедренного треугольника, AM⊥BC.AM\perp BC.

Поскольку AM⊥BCAM\perp BC и OMOM — проекция A1MA_1M на плоскость основания, то по обратной теореме о трёх перпендикулярах A1M⊥BC.A_1M\perp BC.

По теореме о перпендикулярности прямой и плоскости получаем: BC⊥(AA1M1M),BC\perp (AA_1M_1M), следовательно BC⊥AA1BC\perp AA_1 (по определению прямой и плоскости), поэтому стороны BCBC и AA1AA_1 перпендикулярны.

б) Докажем, что четырехугольник CC1B1BCC_1B_1B является прямоугольником.

Поскольку BC⊥AA1BC\perp AA_1 и AA1∥CC1∥BB1,AA_1\parallel CC_1 \parallel BB_1, то BC⊥BB1BC\perp BB_1 и BC⊥CC1.BC\perp CC_1. Следовательно, CC1B1BCC_1B_1B — прямоугольник.