15. Основанием ABCD наклонной призмы ABCDA1B1C1D1 является квадрат с центром О и стороной 2 см. Найдите боковое ребро призмы, учитывая, что A1О = √2 см, а расстояние между плоскостями оснований равно √2 см.

Решение:

Поскольку расстояние между плоскостями оснований есть минимальным расстоянием между точками этих плоскостей и по условию задачи равно $\sqrt{2}\,см,$ а точки $A_1$ и $O$ лежат в этих плоскостях и расстояние между ними также равно $\sqrt{2}\,см,$ то $A_1O\perp (ABCD)$ и есть расстоянием между плоскостями оснований наклонной призмы (см. рис.).

$AO=\dfrac{1}{2}\cdot \sqrt{2}\cdot AD=\dfrac{1}{2}\cdot \sqrt{2}\cdot 2=\sqrt{2}\,см$ — как половина диагонали квадрата.

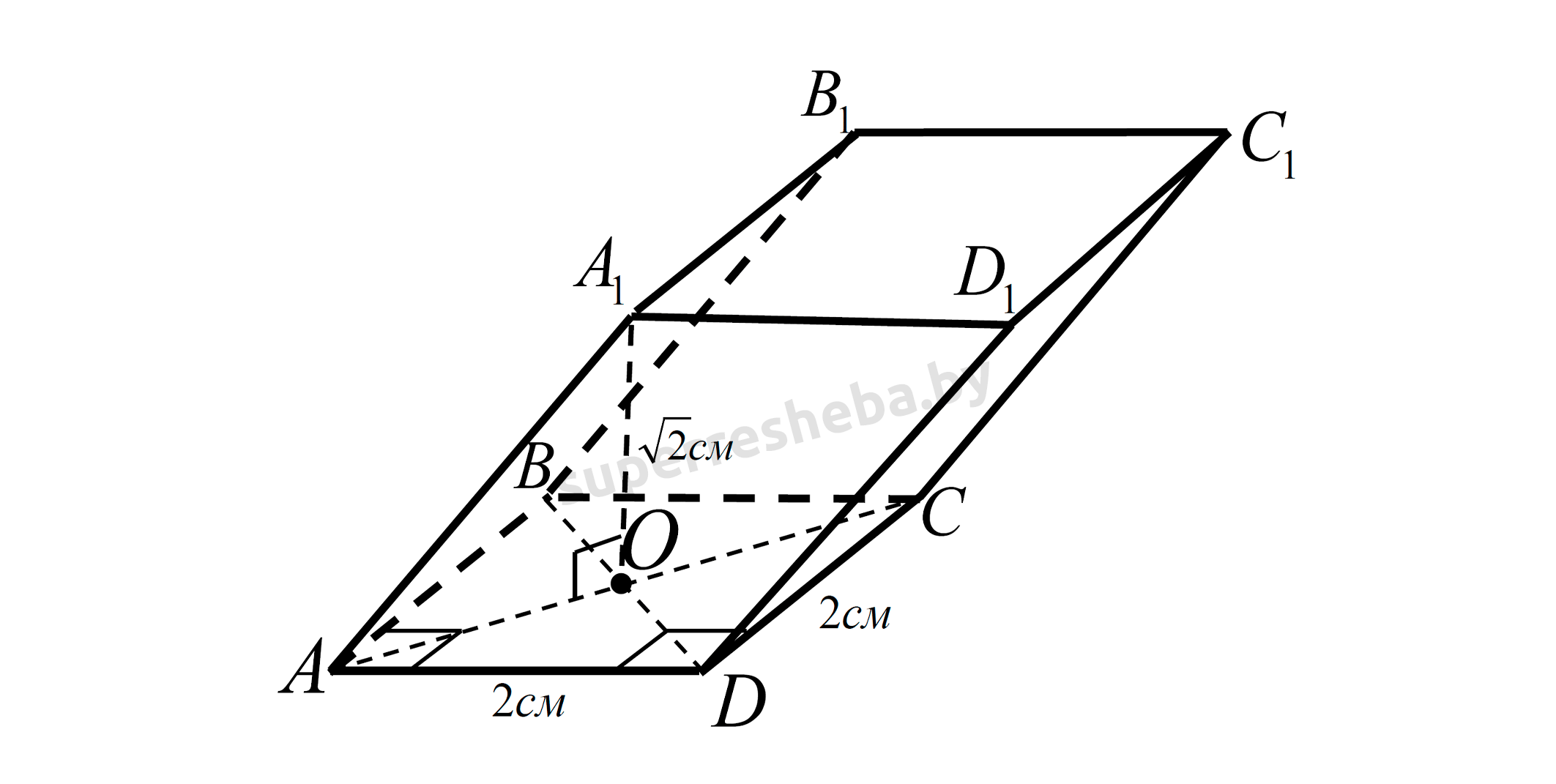
С прямоугольного $\Delta AOA_1, \angle AOA_1=90°$ по теореме Пифагора, получаем:

$AA_1^2=AO^2+A_1O^2;$

$AA_1=\sqrt{AO^2+A_1O^2}=\sqrt{(\sqrt{2}^2+(\sqrt{2})^2}=2\,(см).$

Ответ: $AA_1=2\,см.$