11. В прямоугольном параллелепипеде диагональ образует с плоскостью основания угол в 60°. Найдите диагональ параллелепипеда, учитывая, что радиус окружности, описанной около основания, равен 3 см.

Решение:

Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1ABCDA_1B_1C_1D_1 (см. рис.).

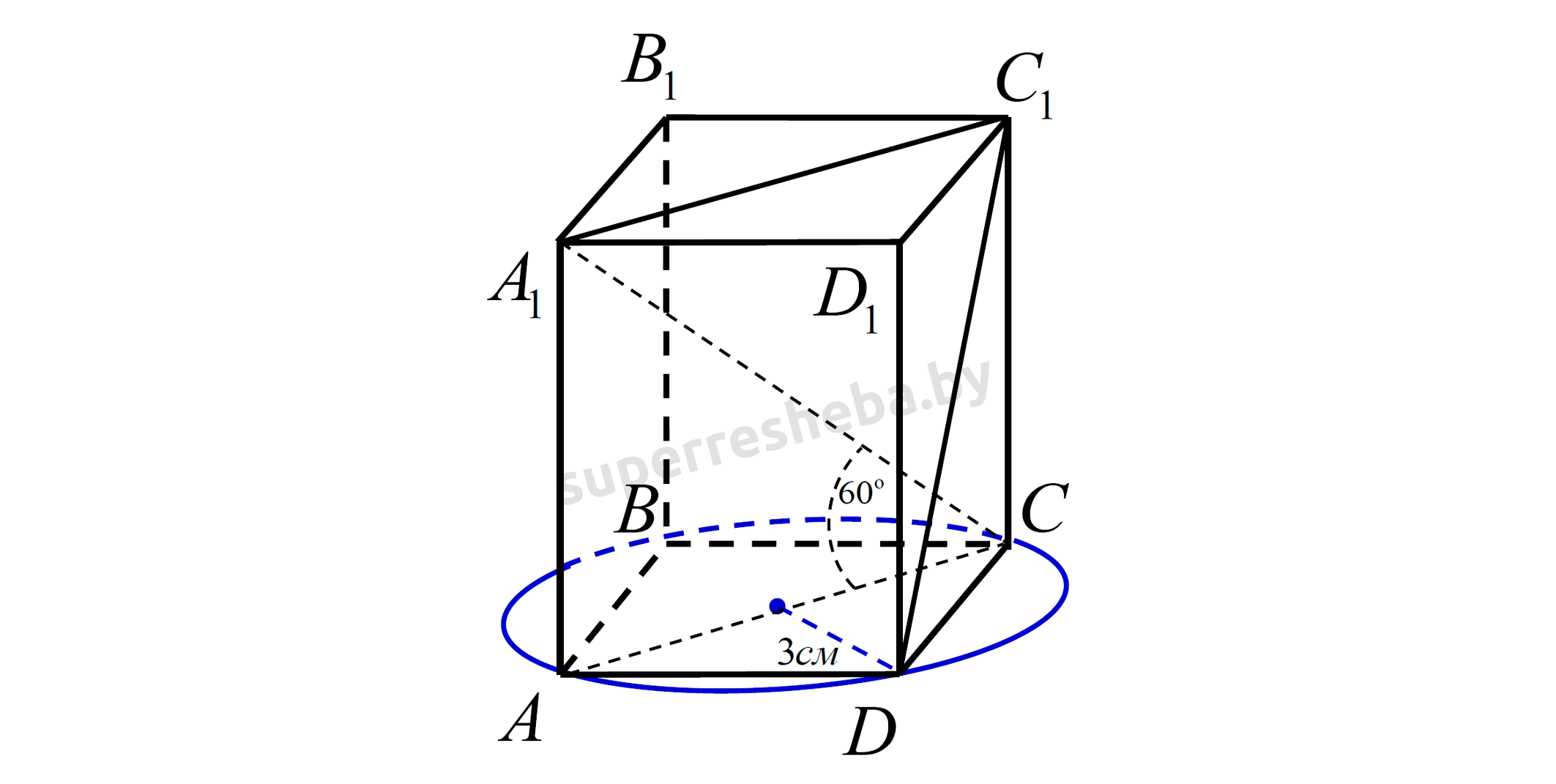
В основании прямоугольный параллелепипед лежит прямоугольник, а радиус окружности описанной вокруг прямоугольника равен половине диагонали прямоугольника, поэтому:

AC=2⋅R=2⋅3=6 см.AC=2\cdot R=2\cdot 3=6\,см.

Тогда с прямоугольного ΔA1AC,∠A1AC=90°,AC=6 см:\Delta A_1AC, \angle A_1AC=90°, AC=6\,см:

A1C=ACcos⁡60°=6cos⁡60°=12 (см).A_1C=\dfrac{AC}{\cos 60°}=\dfrac{6}{\cos 60°}=12\,(см).

Ответ: A1C=12 см.A_1C=12\,см.