9. Найдите диагональ правильной четырехугольной призмы, у которой площадь основания равна 121 см^2 , а высота — 12 см.

Решение:

Рассмотрим рисунок. Поскольку в основании правильной четырехугольной призмы лежит квадрат, то площадь основания правильной четырехугольной призмы:

S=AD⋅DC=a2.S=AD\cdot DC={{a}^{2}}.

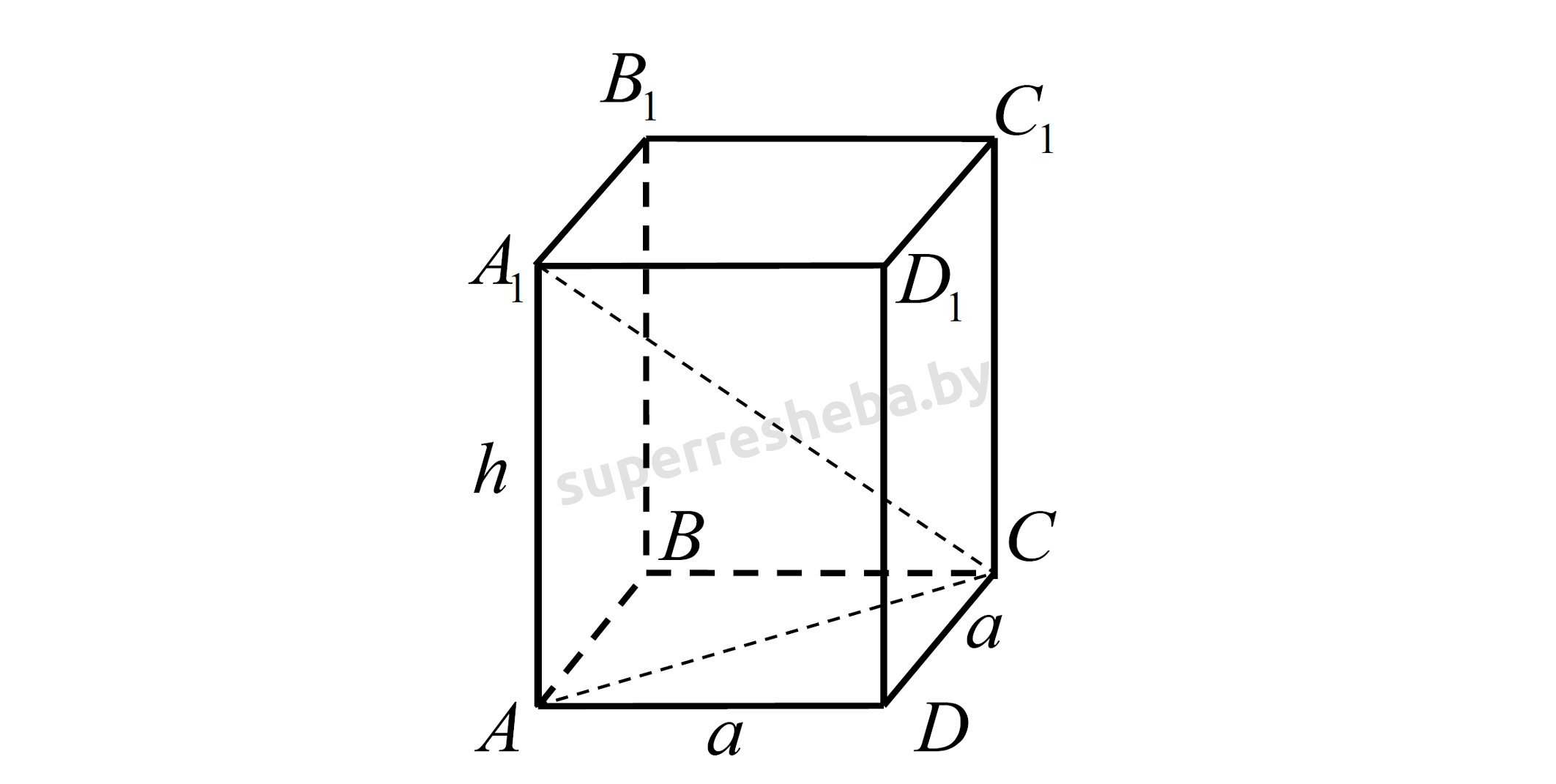
C прямоугольного ΔADC,∠AD=90°,AD=DC=a:\Delta ADC, \angle AD=90°, AD=DC=a:

AС2=AD2+DC2=a2+a2=2a2=2S=2⋅121=242(см2).AС^{2}={{AD}^{2}}+D{{C}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}}=2S=2\cdot 121=242\left( {см^{2}} \right).

C прямоугольного ΔA1AC,∠A1A=90°,AA1=h=12 см:\Delta {{A}_{1}}AC, \angle {{A}_{1}}A=90°, A{{A}_{1}}=h=12\, см:

A1C=AC2+AA12=242+122=386(см).{{A}_{1}C}=\sqrt{{{AC}^{2}}+AA_1^2}=\sqrt{242+{{12}^{2}}}=\sqrt{386}\left( см \right).

Ответ: A1C=386(см).A_1C=\sqrt{386}\left( см \right).