8. Верно ли, что у прямоугольного параллелепипеда: а) есть три оси симметрии; б) есть три плоскости симметрии; в) квадрат диагонали равен сумме квадратов трех его измерений; г) все четыре диагонали равны друг другу; д) с двумя равными измерениями есть пять плоскостей симметрии; е) с тремя равными измерениями есть девять плоскостей симметрии; ж) с тремя равными измерениями есть девять осей симметрии?

Если параллелепипед прямоугольный, то у него будет три оси симметрии. Это прямые, которые проходят через точки пересечения диагоналей противоположных граней.

Утверждение а) верно.

Три плоскости перпендикулярные осям симметрии прямоугольного параллелепипеда, которые проходят через середины отрезков, соединяющих середины противоположных граней параллелепипеда, будут его плоскостями симметрии.

Утверждение б) верно.

Рассмотрим прямой параллелепипед $ABCDA_1B_1C_1D_1$ (см. рис.). Введём обозначения измерений прямоугольного параллелепипеда $AD=a; DC=b; AA_1=c.$ С прямоугольного $\triangle ADC, \angle ADC=90°:$

$AC^2=AD^2+DC^2=a^2+b^2.$

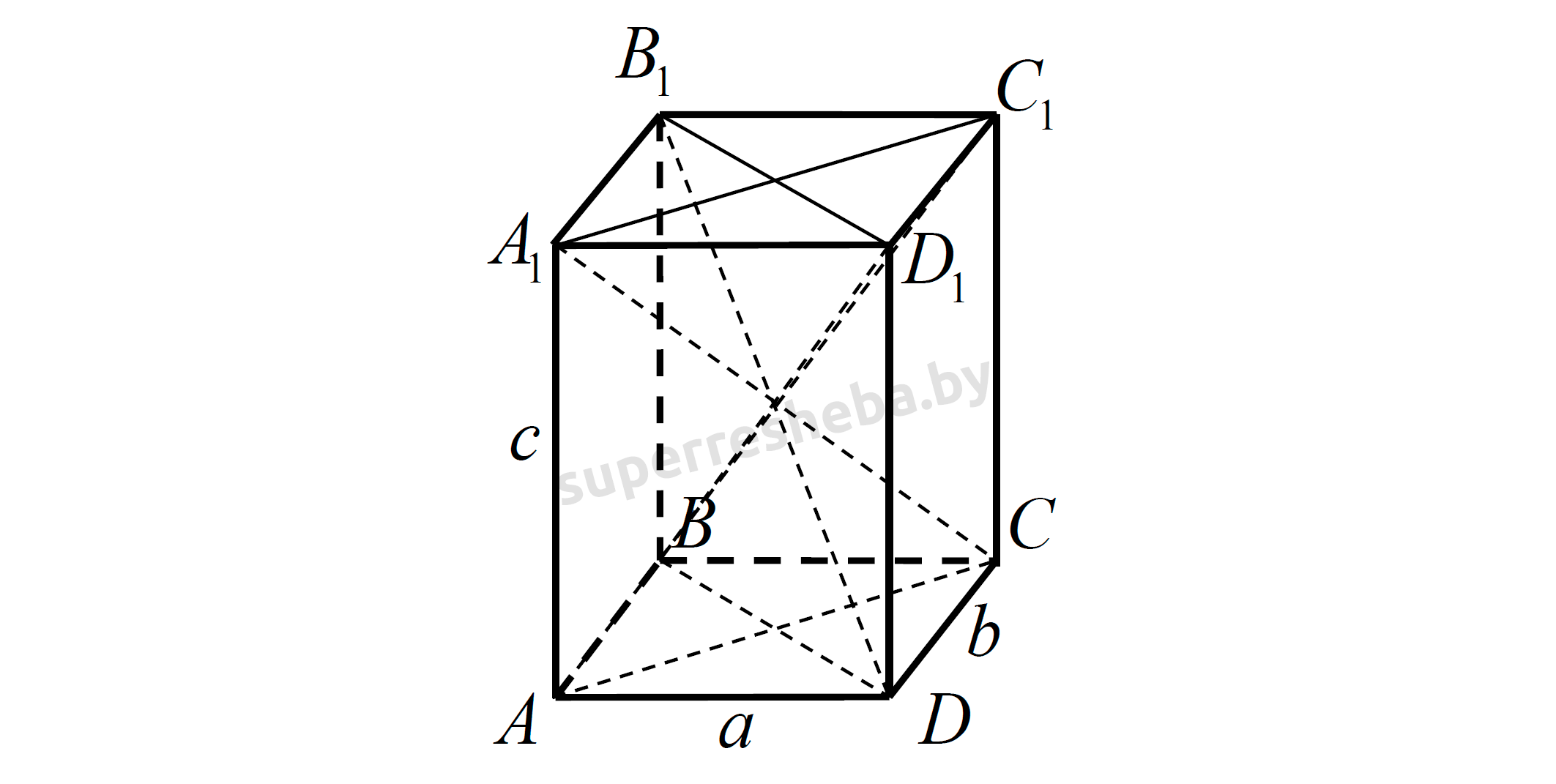
C прямоугольного $\triangle A_1AC, \angle A_1AC=90°:$

$A_1C^2=AC^2+AA_1^2=a^2+b^2+c^2.$

Утверждение в) верно.

Учитывая равенство треугольников $\triangle A_1AC=\triangle B_1BD=\triangle C_1CA=\triangle D_1DB$ (по двум сторонами углу между ними), можно утверждать, что четыре диагонали прямоугольного параллелепипеда равны друг другу.

Утверждение г) верно.

Если 2 измерения прямоугольного параллелепипеда равны, то кроме трёх существующих осей симметрии добавляется ещё 2 плоскости, проходящие через диагонали квадратов (прямоугольников с равными измерениями).

Утверждение д) верно.

Прямоугольный параллелепипед с тремя равными измерениями — куб. Куб имеет девять плоскостей симметрии. Три плоскости симметрии имеет любой прямоугольный параллелепипед и кроме трёх существующих осей симметрии добавляется ещё по 3 пары плоскостей, проходящих через диагонали противоположных граней.

Утверждение е) верно.

Ось симметрии куба может проходить либо через середины параллельных ребер, не принадлежащих одной грани, либо через точку пересечения диагоналей противоположных граней. Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят 9 осей симметрии.

Утверждение ж) верно.

Ответ: а) верно; б) верно; в) верно; а) верно; г) верно; д) верно; е) верно; ж) верно.