7. Верно ли, что у прямого параллелепипеда есть: а) ось симметрии; б) плоскость симметрии?

Рассмотрим рис., на котором покажем прямой параллелепипед ABCDA₁B₁C₁D₁. Прямая OO₁, которая проходит через точку пересечения диагоналей оснований прямого параллелепипеда будет его осью симметрии, поскольку после поворота прямого параллелепипеда вокруг этой прямой на 180° получаем этот же параллелепипед.

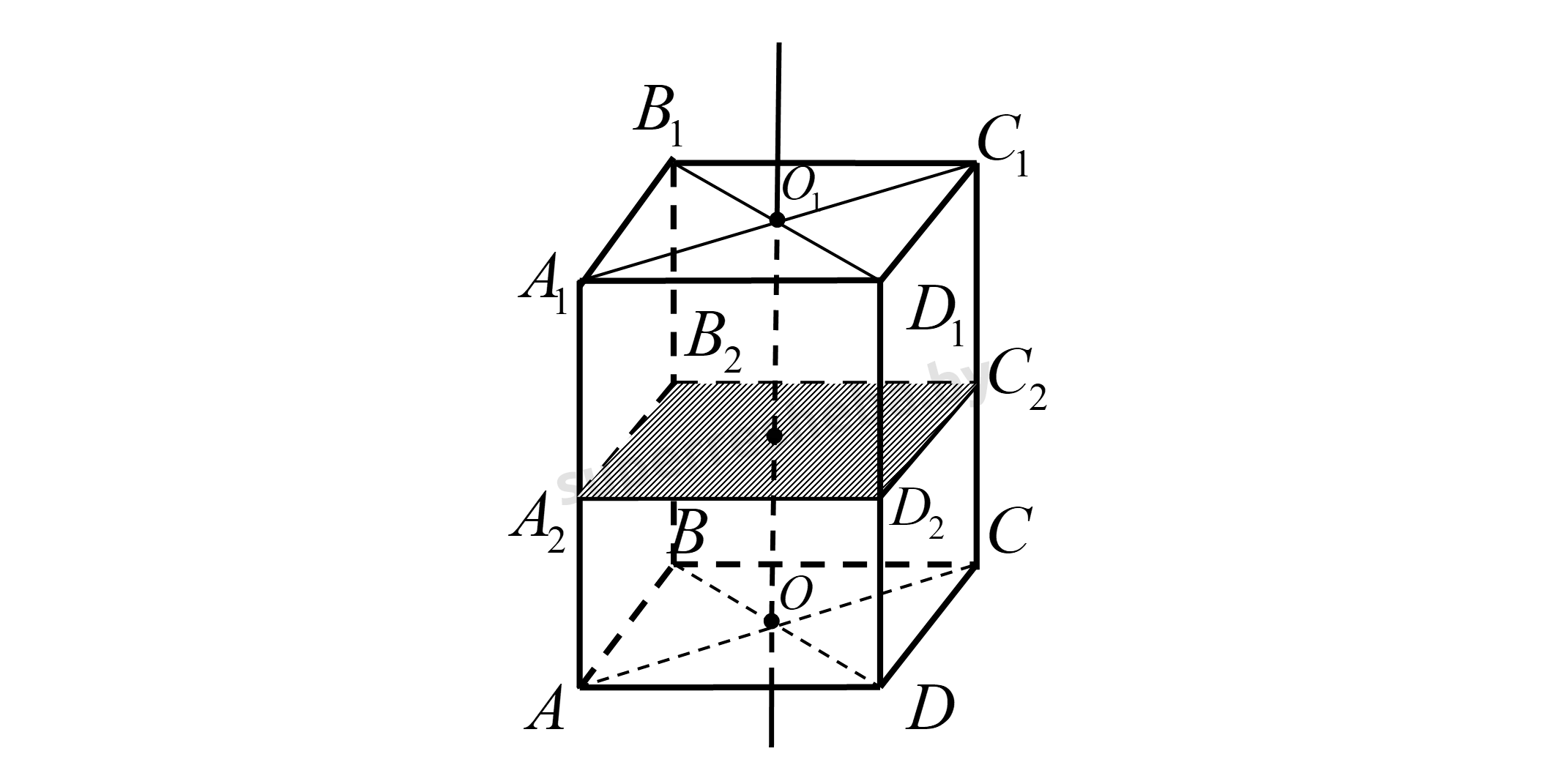
Утверждение а) верно.

Плоскость параллельная основаниям которая проходит через середину отрезка OO₁, будет плоскостью симметрии, поскольку при симметрии относительно этой плоскости точки над плоскостью параллелепипеда переходят в соответствующие точки под плоскостью, а точки под плоскостью переходят в соответствующие точки над плоскостью. Прямой параллелепипед отображается в этот же параллелепипед.

Утверждение б) верно.

Ответ: а) верно; б) верно.