5. Верно ли, что у параллелепипеда: а) есть три четверки равных ребер; б) есть три пары равных граней; в) его четыре диагонали пересекаются в одной точке, являющейся центром симметрии параллелепипеда?

Рассмотрим параллелепипед рисунок. Покажем равные рёбра одинаковым цветом:

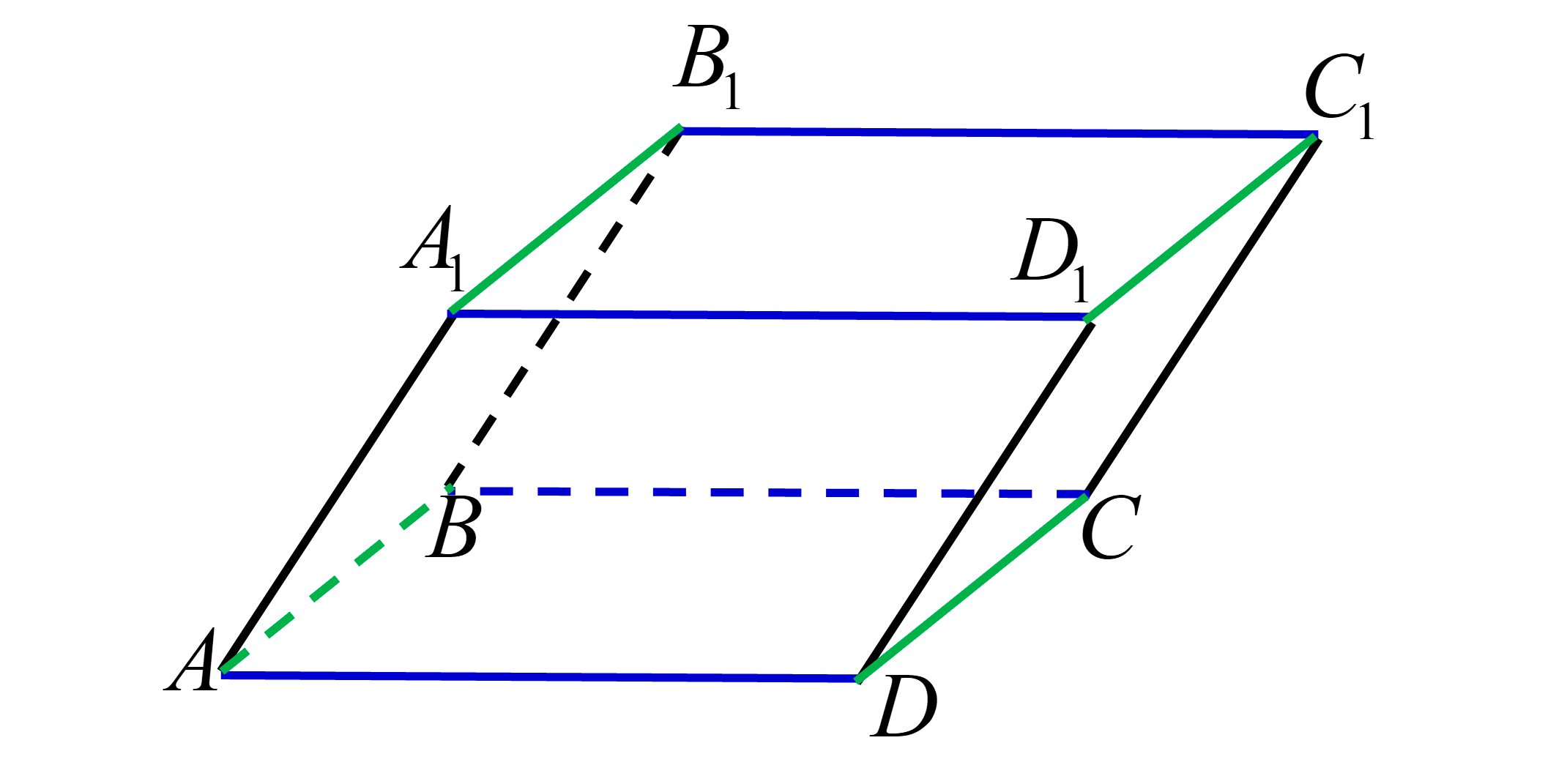
На рисунке видно, что у параллелепипеда есть три четверки равных рёбер.

Утверждение а) верно.

Грани: ABCD и A₁B₁C₁D₁; AA₁B₁B и DD₁C₁C; AA₁D₁D и BB₁C₁C попарно совмещаются параллельными переносами, поэтому они равны.

Утверждение б) верно.

AB || DC и D₁C₁ || DC, поэтому AB || D₁C₁. Через AB и D₁C₁ проведем плоскость, тогда ABC₁D₁ — параллелограмм. Его диагонали AC₁ и BD₁, являющиеся диагоналями параллелепипеда, в точке пересечения делятся пополам. Теперь возьмем одну из этих диагоналей, например AC₁ и третью диагональ параллелепипеда A₁C. Они являются диагоналями параллелограмма AA₁C₁C и поэтому A₁C проходит через середину AC₁, то есть три диагонали параллелепипеда пересекаются в одной точке и делятся в ней пополам. Аналогично доказывается и для четвертой диагонали B₁D.

Следовательно, четыре диагонали пересекаются в одной точке, являющейся центром симметрии параллелепипеда.

Утверждение в) верно.

Ответ: а) верно; б) верно; в) верно.