4. Человек, глаза которого находятся на высоте h = 1,48 м над полом, стоит перед плоским вертикальным зеркалом на расстоянии l = 2,70 м от него. Нижний край зеркала расположен на высоте a = 40 см над полом. На каком расстоянии b от зеркала находится ближайшая точка, которую видно в него?

Дано:

h=1.48 м;h=1.48\,м;

l=2.70 м;l=2.70\,м;

a=40 см=0.4 м.a=40\,см=0.4\,м.

Найти:

b−?b-?

Решение:

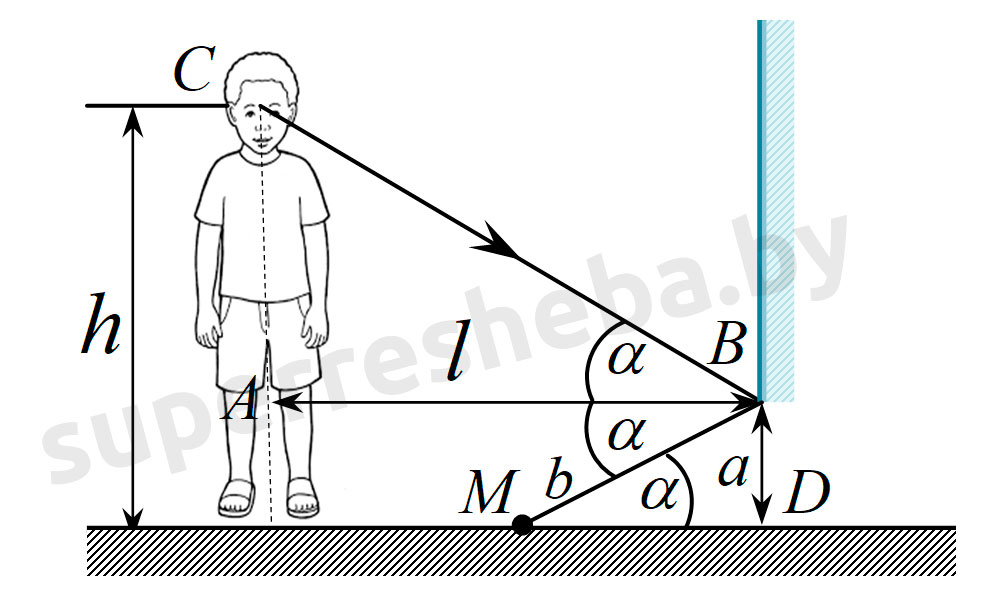
Рассмотрим рисунок. △ABC∽△DMB\triangle ABC \backsim \triangle DMB по двум углам, поэтому соответствующие стороны этих треугольников пропорциональны:

ACDB=CBBM,\dfrac{AC}{DB}=\dfrac{CB}{BM},

где AC=h−a,DB=aAC=h-a, DB=a, по теореме Пифагора CB=(h−a)2+l2,BM=bCB=\sqrt{(h-a)^2+l^2}, BM=b — расстояние от ближайшей к зеркалу точке, которую видно в него.

После подстановки в пропорцию соответствующих длин отрезков, получаем:

h−aa=(h−a)2+l2b;\dfrac{h-a}{a}=\dfrac{\sqrt{(h-a)^2+l^2}}{b};

b=a(h−a)2+l2h−a.b=\dfrac{a\sqrt{(h-a)^2+l^2}}{h-a}.

Подставим численные значения и произведём вычисления:

b=0.4⋅(1.48−0.4)2+2.7021.48−0.4≈1 м.b=\dfrac{0.4\cdot \sqrt{(1.48-0.4)^2+2.70^2}}{1.48-0.4}\approx 1\,м.

Ответ: b=1 м.b=1\,м.