5. Определите напряжение U на конденсаторе емкостью C в момент времени: а) t_1 = T/8 ; б) t_2 = 5T/8 , если в начальный момент времени t_0 = 0 напряжение на конденсаторе равно U_0 = 48 B, а сила тока в катушке I_0 = 0, Т — период колебаний в контуре.
Дано:
t1=8T;
t2=85T;
t0=0;
U0=48В;
I0=0.
Найти:
U1−?
U2−?
Решение:
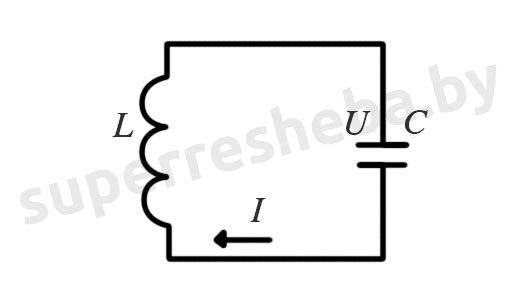
Как следует из условия задачи, напряжение на обкладках конденсатора в колебательном контуре изменяется со временем по закону:
U=U0cosωt,
где ω — циклическая частота свободных электромагнитных колебаний в контуре.
Циклическая частота находится по формуле:
ω=T2π.
Тогда:
U=U0cos(T2πt);
U1=U0cos(T2πt1)=U0cos(T2π⋅8T);
U1=U0cos4π;
U2=U0cos(T2πt2)=U0cos(T2π⋅85T);
U2=U0cos45π.
Вычислим:
U1=U0⋅cos4π≈0.71U0;
U2=U0⋅cos45π≈−0.71U0.
Ответ: а) U=0.71U0; б) U=−0.71U0.
