7. Пружинный маятник, находящийся на гладкой горизонтальной поверхности, вывели из положения равновесия и без толчка отпустили. Через какую часть п периода Т кинетическая энергия прикрепленного к пружине тела будет равна потенциальной энергии W_п деформированной пружины?
Дано:
Найти:
Решение:
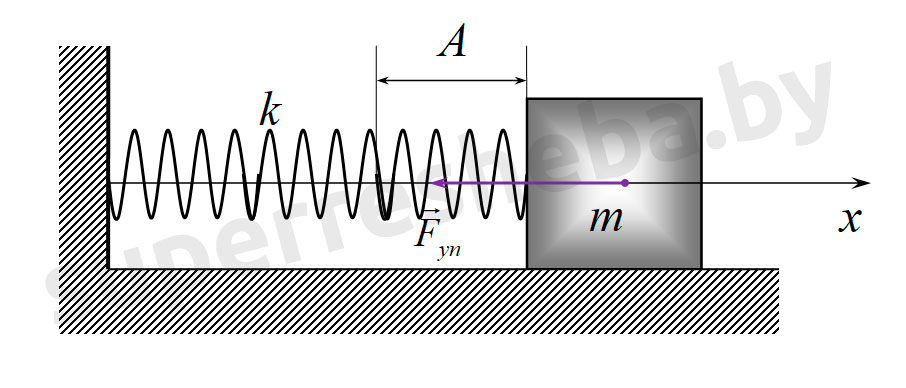
Запишем общий вид уравнения гармонических колебаний пружинного маятника:
По условию задачи отклонение в начальный момент времени равно амплитуде колебаний. Запишем уравнение колебаний для начального момента времени и найдём начальную фазу колебаний:
Тогда уравнения гармонических колебаний пружинного маятника примет вид:
Полную энергию колебаний вычислим по формуле:
Кинетическую энергию для момента времени, в который определяется потенциальная энергия, вычислим по формуле:
По условию задачи тогда
Подставим в уравнение гармонических колебаний маятника:
Учитывая, что циклическая частота вычисляется по формуле получим:
Ответ: