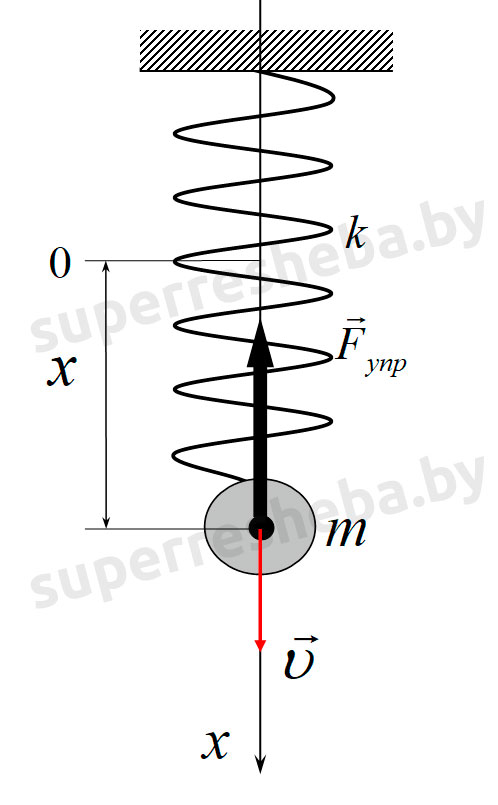
4. Тело совершает гармонические колебания. Определите отношение кинетической энергии к ее потенциальной энергии для моментов времени, когда смещение тела от положения равновесия составляет: а) x = A/2; б) x = 3A/4; в) x = A.
Дано:
а ) x = A 2 ; а)\, x=\dfrac{A}{2}; а ) x = 2 A ;
б ) x = 3 A 4 ; б)\, x=\dfrac{3A}{4}; б ) x = 4 3 A ;
в ) x = A . в)\, x=A. в ) x = A .
Найти:
W к W п − ? \dfrac{W_к}{W_п}-? W п W к − ?
Решение:
Вычислим потенциальную энергию по формуле:
W п = k x 2 2 , W_п=\dfrac{kx^2}{2}, W п = 2 k x 2 ,
где k k k — коэффициент упругости пружинного маятника, x x x — коэффициент упругости пружинного маятника.
Полная энергия колебаний вычисляется по формуле:
W мех = k A 2 2 . W_{мех}=\dfrac{kA^2}{2}. W мех = 2 k A 2 .
Кинетическая энергия для момента времени, в который определяется потенциальная энергия, вычисляется по формуле:
W к = W мех − W п ; W_к=W_{мех}-W_п; W к = W мех − W п ;
W к = k A 2 2 − k x 2 2 ; W_к=\dfrac{kA^2}{2}-\dfrac{kx^2}{2}; W к = 2 k A 2 − 2 k x 2 ;
W к = k ( A 2 − x 2 ) 2 . W_к=\dfrac{k(A^2-x^2)}{2}. W к = 2 k ( A 2 − x 2 ) .
Найдём отношение кинетической энергии к потенциальной:
W к W п = k ( A 2 − x 2 ) 2 : k x 2 2 ; \dfrac{W_к}{W_п}=\dfrac{k(A^2-x^2)}{2}:\dfrac{kx^2}{2}; W п W к = 2 k ( A 2 − x 2 ) : 2 k x 2 ;
W к W п = k ( A 2 − x 2 ) 2 ⋅ 2 k x 2 ; \dfrac{W_к}{W_п}=\dfrac{k(A^2-x^2)}{2}\cdot \dfrac{2}{kx^2}; W п W к = 2 k ( A 2 − x 2 ) ⋅ k x 2 2 ;
W к W п = k ( A 2 − x 2 ) k x 2 ; \dfrac{W_к}{W_п}=\dfrac{k(A^2-x^2)}{kx^2}; W п W к = k x 2 k ( A 2 − x 2 ) ;
W к W п = A 2 − x 2 x 2 ; \dfrac{W_к}{W_п}=\dfrac{A^2-x^2}{x^2}; W п W к = x 2 A 2 − x 2 ;
W к W п = ( A x ) 2 − 1. \dfrac{W_к}{W_п}=\left(\dfrac{A}{x}\right)^2-1. W п W к = ( x A ) 2 − 1.
а) при x = A 2 x=\dfrac{A}{2} x = 2 A получим:
W к W п = ( A A 2 ) 2 − 1 = 2 2 − 1 = 3. \dfrac{W_к}{W_п}=\left(\dfrac{A}{\dfrac{A}{2}}\right)^2-1=2^2-1=3. W п W к = ⎝ ⎛ 2 A A ⎠ ⎞ 2 − 1 = 2 2 − 1 = 3.
б) при x = 3 A 2 x=\dfrac{3A}{2} x = 2 3 A получим:
W к W п = ( A 3 A 4 ) 2 − 1 = ( 4 3 ) 2 − 1 = 7 9 ≈ 0.78. \dfrac{W_к}{W_п}=\left(\dfrac{A}{\dfrac{3A}{4}}\right)^2-1=\left(\dfrac{4}{3}\right)^2-1=\dfrac{7}{9}\approx0.78. W п W к = ⎝ ⎛ 4 3 A A ⎠ ⎞ 2 − 1 = ( 3 4 ) 2 − 1 = 9 7 ≈ 0.78.
в) при x = A x=A x = A получим:
W к W п = ( A A ) 2 − 1 = 1 2 − 1 = 0. \dfrac{W_к}{W_п}=\left(\dfrac{A}{A}\right)^2-1=1^2-1=0. W п W к = ( A A ) 2 − 1 = 1 2 − 1 = 0.
Ответ: а ) 3 ; б ) 0.78 ; в ) 0. а)\, 3; б)\, 0.78; в)\, 0. а ) 3 ; б ) 0.78 ; в ) 0.