3. Математический маятник массой m = 100 г выводят из положения равновесия, поднимая его на высоту h = 10 см над начальным уровнем. Определите: а) изменение потенциальной энергии маятника ΔW_п при его отклонении от положения равновесия; б) его максимальную кинетическую энергию W_к max.

Дано:

g=9.8 мс;g=9.8\,\dfrac{м}{с};

m=100 г=0.1 кг;m=100\,г=0.1\,кг;

h=10 см=0.1 м.h=10\,см=0.1\,м.

Найти:

ΔWп−?\Delta W_п-?

(Wк)max−?(W_к)_{max}-?

Решение:

а)

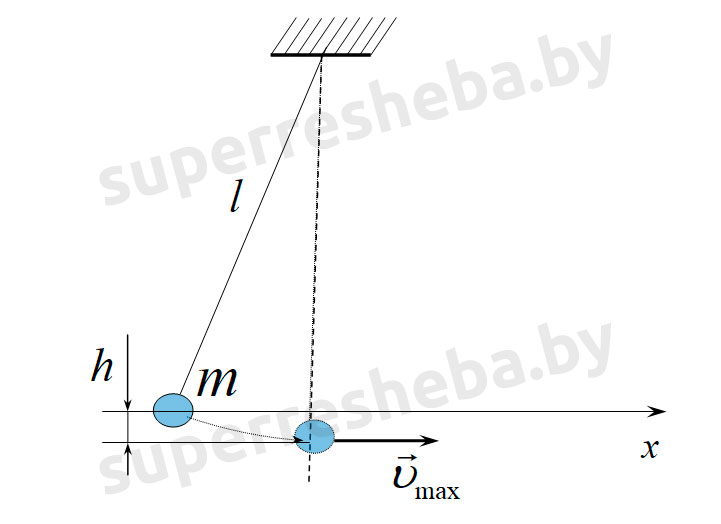
Изменение потенциальной энергии математического маятника вычислим по формуле:

ΔWп=W2−W1;\Delta W_п=W_2-W_1;

ΔWп=0−mgh=−mgh.\Delta W_п=0-mgh=-mgh.

Отрицательный знак указывает на то, что потенциальная энергия уменьшается.

Подставим значения физических величин и вычислим:

ΔWп=−0.1⋅9.8⋅0.1=−0.098 Дж≈−0.10 Дж.\Delta W_п=-0.1\cdot 9.8\cdot 0.1=-0.098\,Дж\approx -0.10\,Дж.

б)

По закону сохранения полной механической энергии максимальная, кинетическая энергия равна начальной потенциальной энергии математического маятника:

(Wк)max=mgh.(W_к)_{max}=mgh.

Подставим значения физических величин и вычислим:

(Wк)max=0.1⋅9.8⋅0.1=0.098 Дж≈0.10 Дж.(W_к)_{max}=0.1\cdot 9.8\cdot 0.1=0.098\,Дж\approx 0.10\,Дж.

Ответ: Wп=−0.10 Дж;(Wк)max=0.10 Дж.W_п=-0.10\,Дж; (W_к)_{max}=0.10\,Дж.