2. Математический маятник массой m = 100 г при прохождении положения равновесия имеет скорость, модуль которой v = 4,0 м/с Определите: а) полную энергию W_мех маятника; б) максимальную высоту h_max, на которую поднимается маятник.

Дано:

$g=9.8\,\dfrac{м}{с};$

$m=100\,г=0.1\,кг;$

$v=4.0\,\dfrac{м}{с}.$

Найти:

$W_{мех}-?$

$h_{max}-?$

Решение:

а) При прохождения маятником положения равновесия его кинетическая энергия $W_к=\dfrac{mv^2}{2}$ максимальна и равна полной энергии:

$W_{мех}=\dfrac{mv^2}{2}.$

Подставим численные значения физических величин и произведём вычисления:

$W_{мех}=\dfrac{0.1\cdot 4^2}{2}=0.8\,Дж.$

б) Учитывая закон сохранения энергии, максимальная кинетическая энергия математического маятника равна максимальной потенциальной энергии $(W_п)_{max}=mgh_{max}$ и равна полной энергии. Следовательно, можно записать:

$W_{мех}=mgh_{max};$

$h_{max}=\dfrac{W_{мех}}{mg}.$

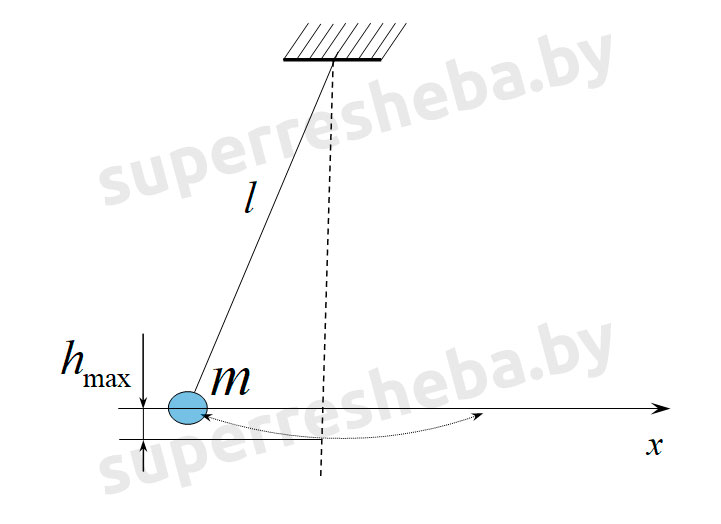
Подставим численные значения физических величин и вычислим максимальную высоту $h_{max},$ на которую поднимется маятник:

$h_{max}=\dfrac{0.8}{0.1\cdot9.8}=0.816\,м=81.6\,см.$

Ответ: а) $W_{мех}=0.8\,Дж;$ б) $h_{max}=81.6\,см.$