7. Период малых колебаний математического маятника на поверхности Земли равен Т = 0,80 с. Каким будет период Т_1 его колебаний на поверхности Марса, если ускорение свободного падения g_м = 0,37g_з?

Дано:

$T=0.80\,с;$

$g_М=0.37\cdot g_З.$

Найти:

$T_1-?$

Решение:

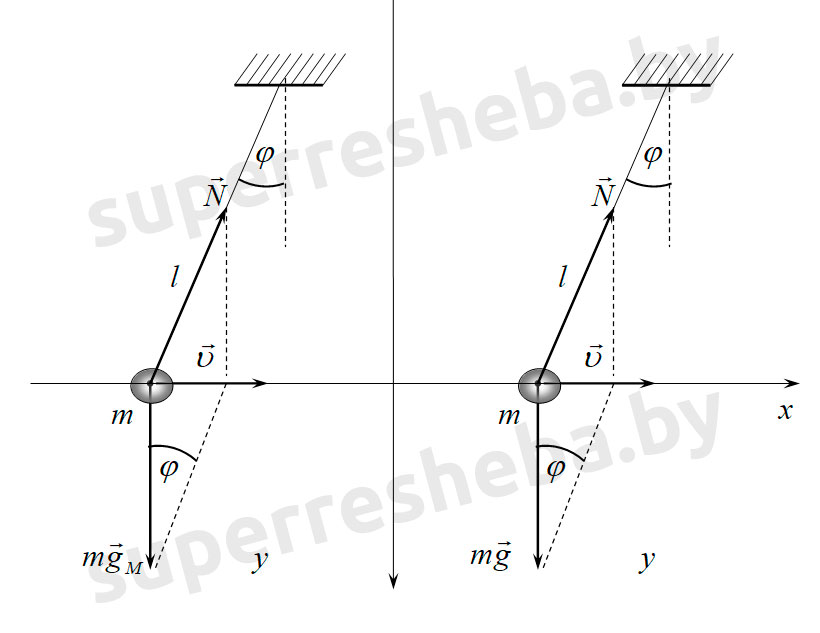
Период колебаний математического маятника вычислим по формуле:

$T=2\pi\sqrt{\dfrac{l}{g_З}},$

где $l$ — длина математического маятника, $g_З$ — ускорение свободного падения на поверхности Земли.

Запишем формулу периода колебаний математического маятника для Марса:

$T_1=2\pi\sqrt{\dfrac{l}{g_М}},$

где $g_М$ — ускорение свободного падения на поверхности Марса.

Разделив первое уравнение на второе, найдём период колебаний заданного математического маятника на Марсе:

$\dfrac{T}{T_1}=\dfrac{2\pi\sqrt{\dfrac{l}{g_З}}}{2\pi\sqrt{\dfrac{l}{g_М}}};$

$\dfrac{T}{T_1}=\sqrt{\dfrac{g_М}{g_З}};$

$T_1=T\sqrt{\dfrac{g_З}{g_М}}.$

Учитывая условие задачи, получим:

$T_1=T\sqrt{\dfrac{g_З}{0.37\cdot g_З}};$

$T_1=T\sqrt{\dfrac{1}{0.37}}.$

Подставим численные значения периода колебаний математического маятника на поверхности Земли и вычислим период колебаний заданного математического маятника на Марсе:

$T_1=0.8\cdot\sqrt{\dfrac{1}{0.37}}=1.3\,с.$

Ответ: $T=1.3\,с.$