4. Груз, подвешенный к пружине, вызывает ее удлинение на величину Δl. Определите Δl пружины, если циклическая частота вертикальных колебаний такой системы ω = 10 рад/с.

Дано:

$\omega=10\dfrac{рад}{с}.$

Найти:

$\Delta l -?$

Решение:

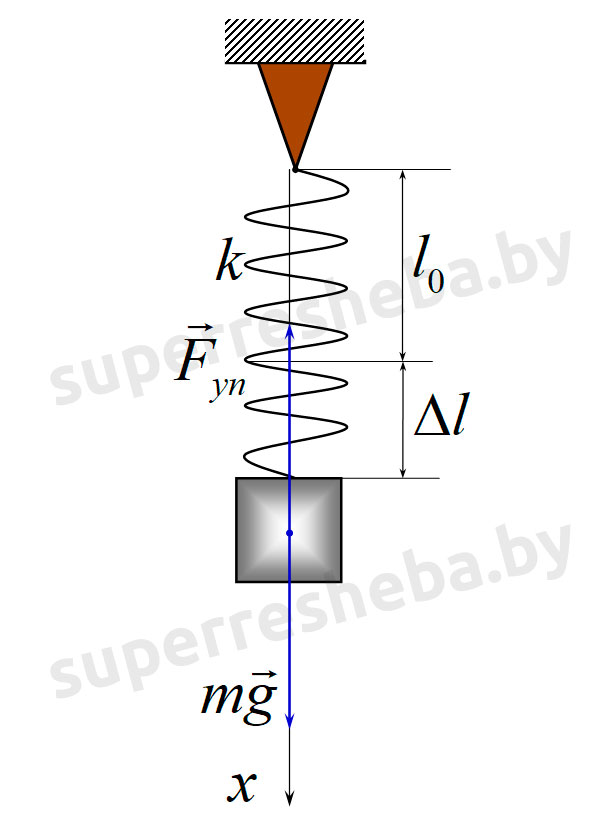
Зададим систему отсчёта. Ось $x$ направим вертикально вниз. Запишем условие равновесия груза подвешенного на пружине:

$\overset{\rightarrow}{F}_{упр}+m\overset{\rightarrow}{g}=0.$

Спроектируем векторы сил на ось $x:$

$-F_{упр}+mg=0.$

$F_{упр}=mg,$

где $F_{упр}=k\Delta l$ — модуль силы упругости, $k$ — жёсткость пружины, $\Delta l$ — удлинение пружины после подвешивания груза, $g=9.8\dfrac{м}{с^2}$ — ускорение свободного падения на поверхности Земли, $m$ — масса подвешенного груза.

После подстановки силы упругости выразим удлинение пружины:

$k\Delta l=mg;$

$\Delta l =\dfrac{m}{k}g.$

Период колебаний пружинного маятника вычислим по формуле:

$T=2\pi\sqrt{\dfrac{m}{k}}.$

Циклическая частота колебаний связана с периодом соотношением:

$\omega=\dfrac{2\pi}{T}.$

После подстановки периода в формулу циклической частоты получим:

$\omega=\dfrac{2\pi}{2\pi\sqrt{\dfrac{m}{k}}};$

$\omega=\dfrac{1}{\sqrt{\dfrac{m}{k}}};$

$\sqrt{\dfrac{m}{k}}=\dfrac{1}{\omega};$

$\dfrac{m}{k}=\dfrac{1}{\omega^2}.$

Подставим последнее отношение в формулу удлинения пружины и получим:

$\Delta l=\dfrac{g}{\omega^2}.$

Подставим численные значения физических величин и вычислим удлинение пружины под действием груза:

$\Delta l=\dfrac{9.8}{10^2}=0.098\,м=9.8\,см\approx 10\,см.$

Ответ: $\Delta l = 10\,см.$