1. Определите период Т и частоту v колебаний груза массой m = 200 г, подвешенного на пружине жесткостью k = 0.15 Н/м

Дано:

$m=200\,г=0.2\,кг;$

$k=0.15\dfrac{Н}{м}.$

Найти:

$T-? \nu-?$

Решение:

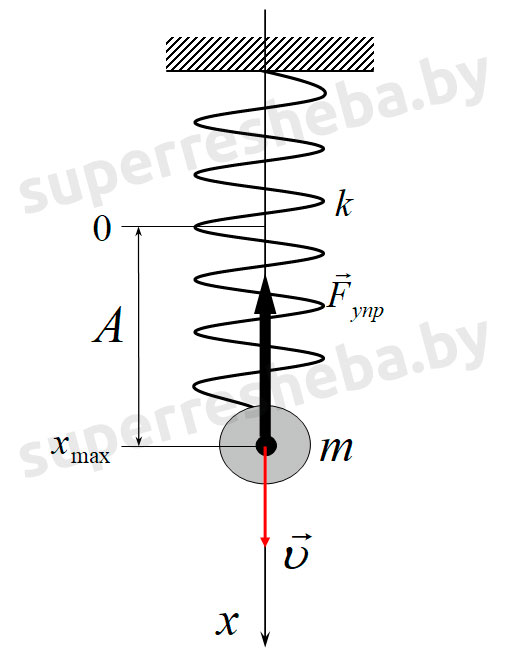
Период колебаний пружинного маятника, вычисляется по формуле:

$T=2\pi\sqrt{\dfrac{m}{k}},$

где $m$ — масса груза маятника, $k$ — коэффициент упругости пружины.

Подставим численные значения физических величин и вычислим период колебаний пружинного маятника:

$T=2\cdot 3.14\cdot\sqrt{\dfrac{0.2}{0.15}}=7.25\,с\approx 7.3\,с.$

Частота колебаний связана с периодом соотношением:

$\nu=\dfrac{1}{T}.$

Подставим численное значение периода и вычислим частоту колебаний пружинного маятника:

$\nu=\dfrac{1}{7.25}=0.14\,Гц.$

Ответ: $T=7.25\,с;\nu=0.14\,Гц.$