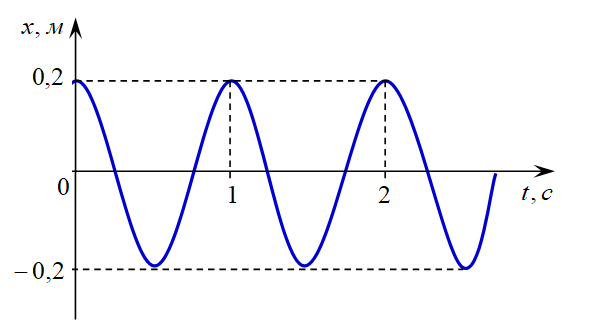
5. Тело колеблется с амплитудой A = 20 см и периодом Т = 1,0 с. Запишите кинематический закон его движения, если в начальный момент времени t = 0 c отклонение маятника максимально. Постройте график зависимости x(t).
Дано:
Найти:
Решение:
Запишем общий вид кинетического закона гармонических колебаний тела:
где — амплитуда колебаний, — циклическая частота колебаний, — период колебаний.
После подстановки циклической частоты получаем:
По условию задачи, в начальный момент времени отклонение маятника максимально:
Тогда вид кинетического закона гармонических колебаний тела примет вид:
Вычислим:
График зависимости
Ответ: