97. Изобразите треугольную пирамиду CDEF и постройте её сечение плоскостью, проходящей через середины рёбер FC, FD, FE. Найдите площадь грани пирамиды, учитывая, что все её грани — равные друг другу правильные треугольники, а площадь сечения равна 120 см2.

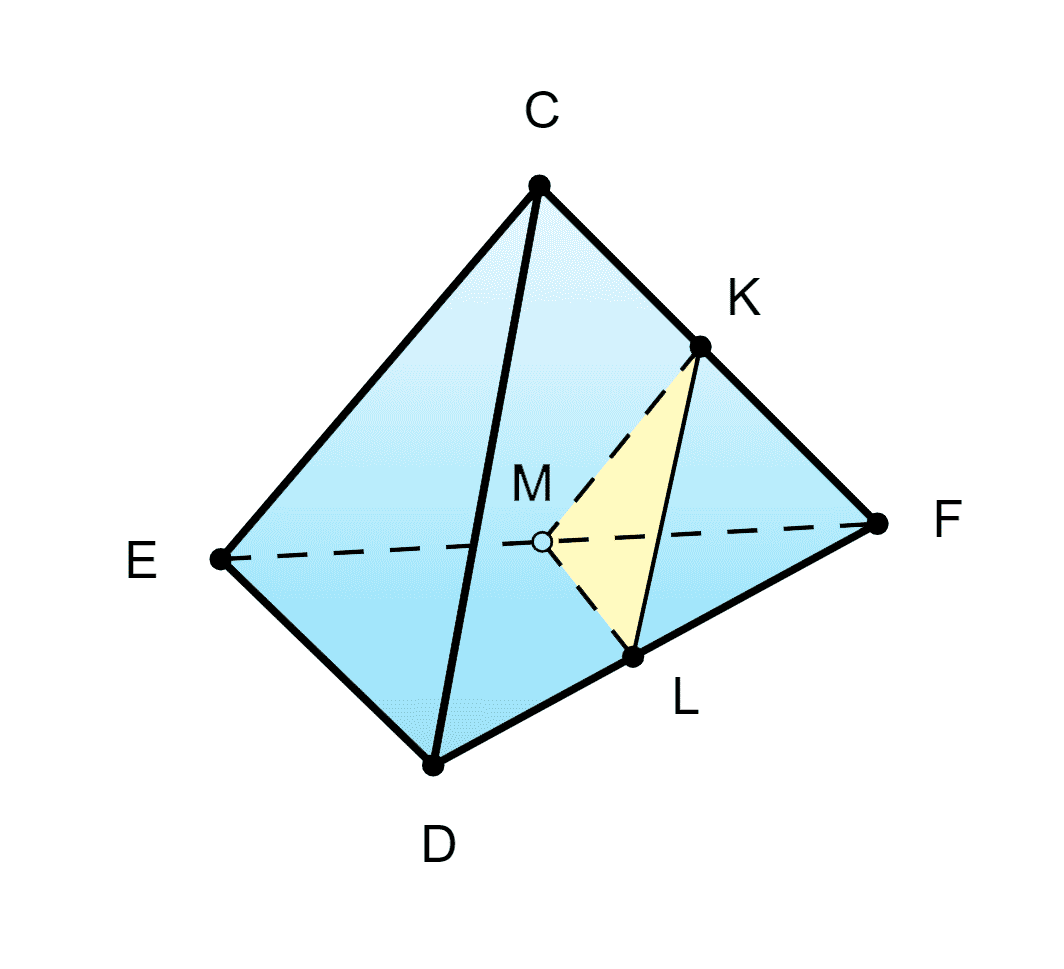
Решение:

По условию все грани пирамиды — правильные треугольники и △ECD∼△MKL\triangle ECD \sim \triangle MKL с коэффициентом подобия k=2,k=2, значит SECD:SMKL=k2.S_{ECD}:S_{MKL}=k^2.

SECD=4⋅120=480 (см2).S_{ECD}=4\cdot 120=480\,(см^2).

Ответ: SECD=480 см2.S_{ECD}=480\,см^2.