90. Имеется пирамида RMNOP, все рёбра которой равны друг другу. Сечением этой пирамиды плоскостью, проходящей через вершину R и прямую NP, является треугольник RNP. Найдите боковую поверхность пирамиды, учитывая, что радиус окружности, описанной около этого треугольника, равен R.
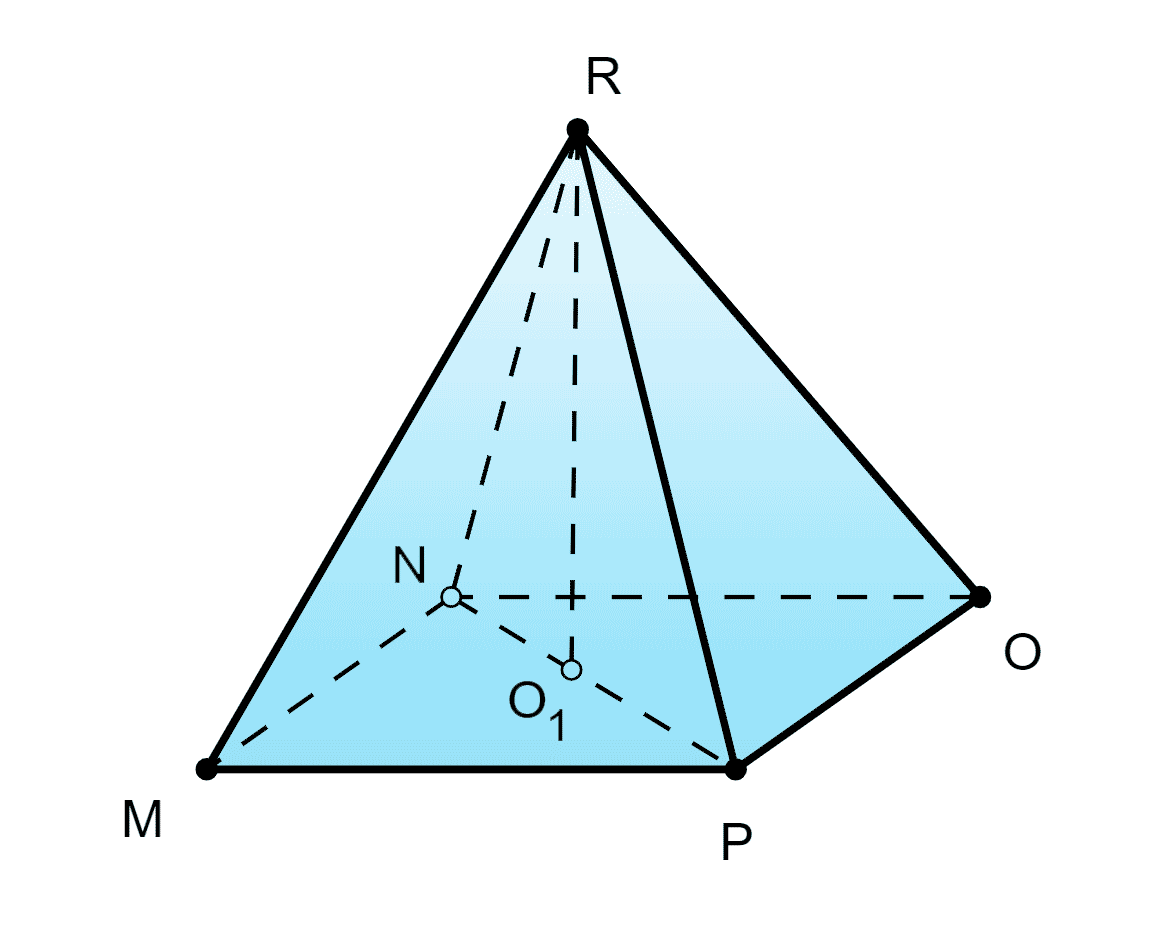
Решение:
Пусть — пирамида, все рёбра которой равны друг другу.
Предположим, каждое ребро равно
Рассмотрим треугольник
— квадрат, значит треугольник — прямоугольный.
По условию (радиус описанной окружности).
Ответ: