88. Изобразите четырёхугольную пирамиду STUVW и постройте её сечение плоскостью, проходящей через точки A, B, C на рёбрах ST, TW, VW.

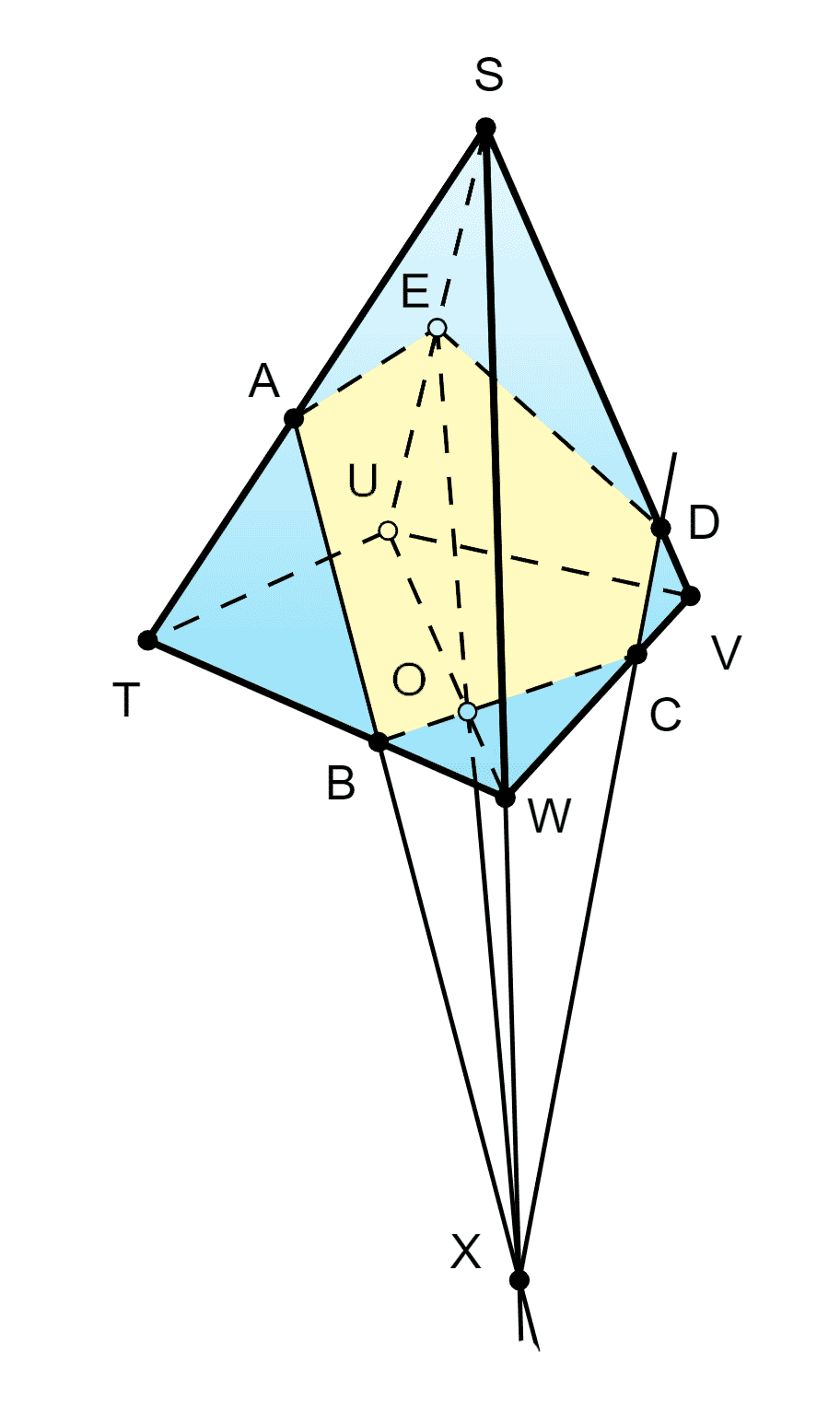
Решение:

Пусть $ABC$ — секущая плоскость, $AB$ и $BC$ — стороны сечения (Аксиома 2).

$AB\cap SW=X;$

$XC$ — след пересечения плоскостей $ABC$ и $SVW;$

$CD$ — сторона сечения (Аксиома 2);

$BC\cap UW=O;$

$XO\cap SU=E.$

По Аксиоме 2 $AE$ и $DE$ — стороны сечения.

$ABCDE$ — искомое сечение.