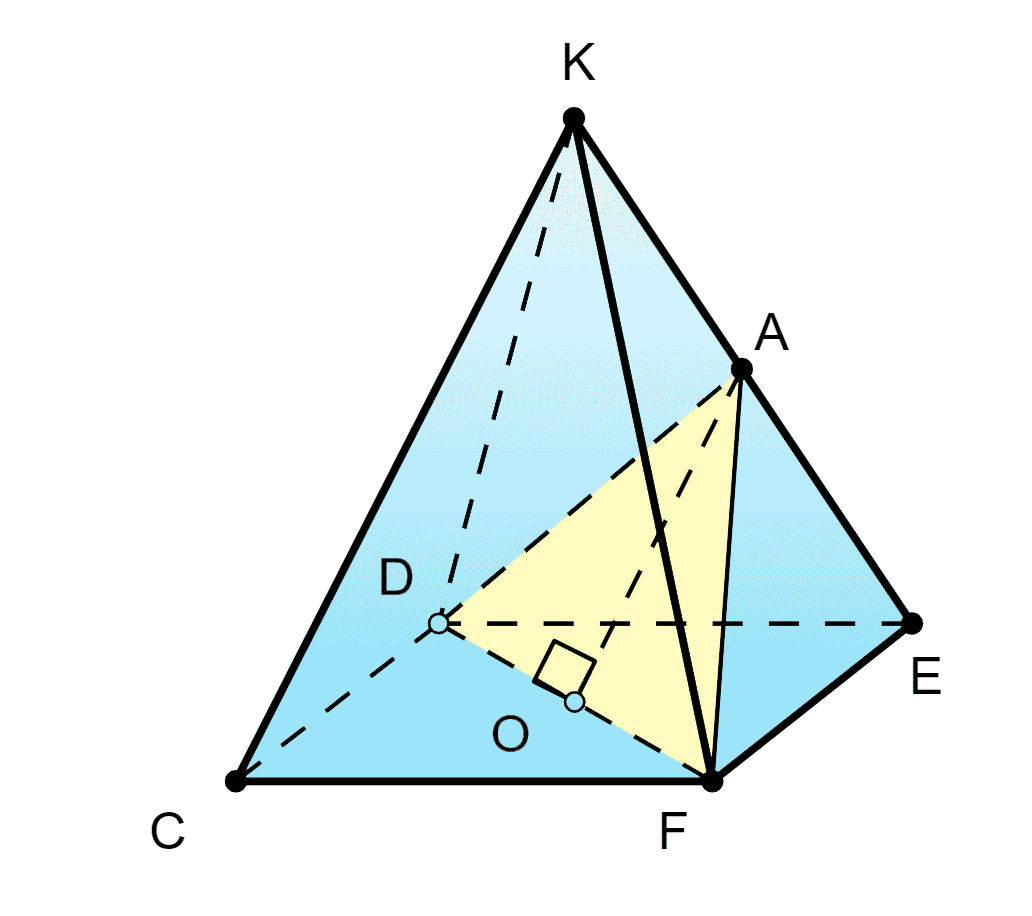
86. Точка A — середина бокового ребра KE правильной четырёхугольной пирамиды KCDEF, все рёбра которой равны друг другу. Постройте сечение пирамиды плоскостью, проходящей через прямую DF и точку A. Найдите полную поверхность пирамиды, учитывая, что площадь этого сечения равна S.
Решение:
K C D E F KCDEF K C D E F — правильная пирамида с равными рёбрами, A K = A E , △ D A F AK=AE, \triangle DAF A K = A E , △ D A F — сечение, S D A F = S . S_{DAF}=S. S D A F = S .
Пусть ребро пирамиды равно a . a. a . Найдём S D A F . S_{DAF}. S D A F .
A D = A F = a 3 2 AD=AF=\dfrac{a\sqrt{3}}{2} A D = A F = 2 a 3 — высота правильного треугольника, D F = a 2 DF=a\sqrt{2} D F = a 2 — диагональ квадрата.
A O = ( a 3 2 ) 2 − ( a 2 2 ) 2 = a 2 ; AO=\sqrt{\left(\dfrac{a\sqrt{3}}{2}\right)^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a}{2}; A O = ( 2 a 3 ) 2 − ( 2 a 2 ) 2 = 2 a ;
S D A F = 1 2 ⋅ D F ⋅ O A = 1 2 a 2 ⋅ a 2 = 1 4 a 2 2 = S S_{DAF}=\dfrac{1}{2}\cdot DF\cdot OA=\dfrac{1}{2}a\sqrt{2}\cdot \dfrac{a}{2}=\dfrac{1}{4}a^2\sqrt{2}=S S D A F = 2 1 ⋅ D F ⋅ O A = 2 1 a 2 ⋅ 2 a = 4 1 a 2 2 = S по условии задачи, откуда
a 2 = 4 S 2 = 2 S ⋅ 2 . a^2=\dfrac{4S}{\sqrt{2}}=2S\cdot \sqrt{2}. a 2 = 2 4 S = 2 S ⋅ 2 .
S п о л н = S о с н + 4 S б о к . г р а н и = a 2 + 4 a 2 3 4 = a 2 ( 1 + 3 ) = 2 S 2 ( 1 + 3 ) = 2 S ( 2 + 6 ) . S_{полн}=S_{осн}+4S_{бок. грани}=a^2+4\dfrac{a^2\sqrt{3}}{4}=a^2\left( 1+\sqrt{3}\right)=2S\sqrt{2}\left( 1+\sqrt{3}\right)=2S\left(\sqrt{2}+\sqrt{6}\right). S п о л н = S о с н + 4 S б о к . г р а н и = a 2 + 4 4 a 2 3 = a 2 ( 1 + 3 ) = 2 S 2 ( 1 + 3 ) = 2 S ( 2 + 6 ) .
Ответ: S п о л н = 2 S ( 2 + 6 ) . S_{полн}=2S\left(\sqrt{2}+\sqrt{6}\right). S п о л н = 2 S ( 2 + 6 ) .