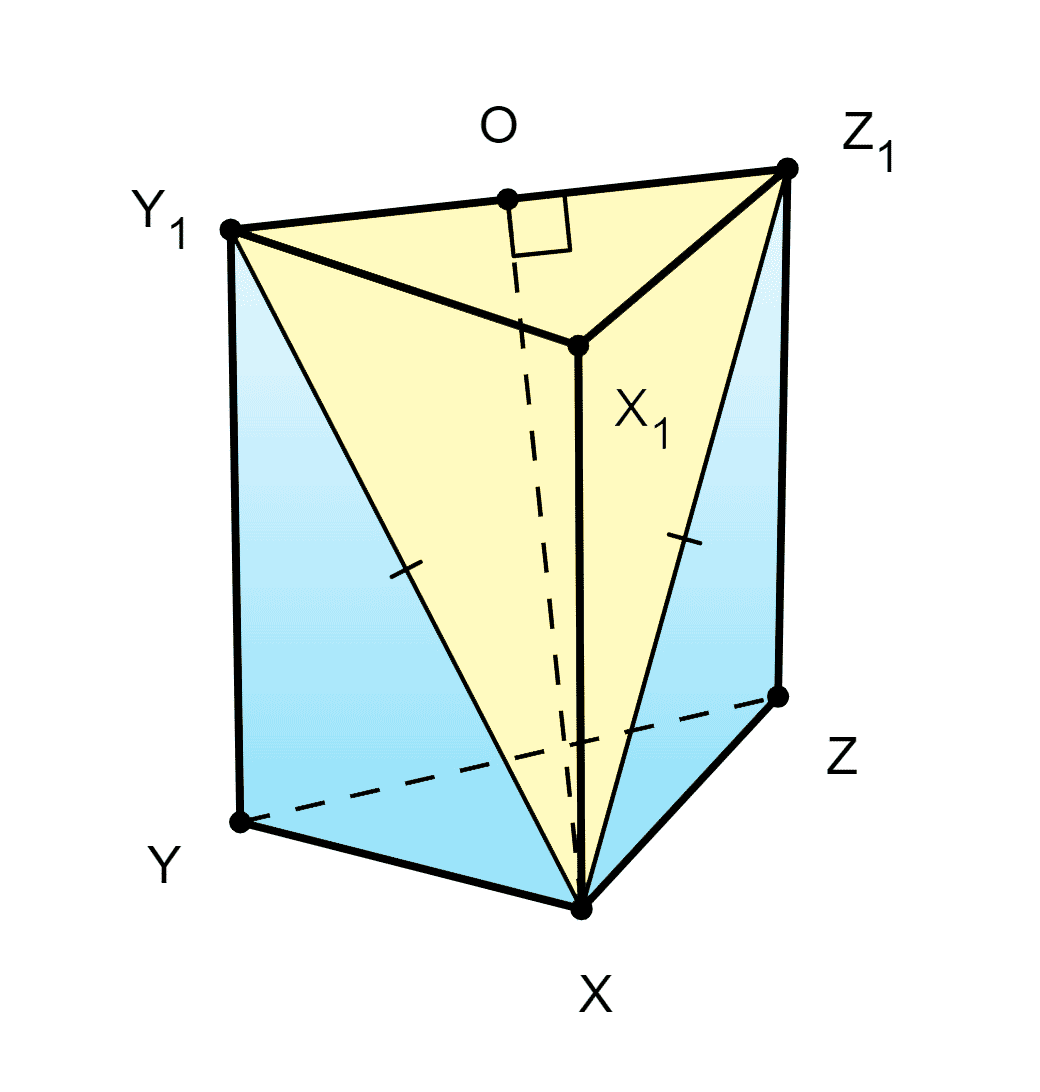83. Дана правильная призма XYZX1Y1Z1, все рёбра которой равны друг другу. Найдите площадь сечения призмы плоскостью XY1Z1, учитывая, что полная поверхность призмы равна S.
Решение:
X Y Z X 1 Y 1 Z 1 XYZX_1Y_1Z_1 X Y Z X 1 Y 1 Z 1 — правильная пирамида, X Y = Y Y 1 , Y 1 X Z 1 XY=YY_1, Y_1XZ_1 X Y = Y Y 1 , Y 1 X Z 1 — сечение.
S п о л н = S . S_{полн}=S. S п о л н = S .
Предположим, ребро призмы равно a , a, a , тогда
S п о л н = 2 S о с н + S б о к ; S_{полн}=2S_{осн}+S_{бок}; S п о л н = 2 S о с н + S б о к ;
S = S п о л н = 2 a 2 3 4 + 3 a 2 = 2 a 2 ( 3 + 6 ) 4 ; S=S_{полн}=\dfrac{2a^2\sqrt{3}}{4}+3a^2=\dfrac{2a^2\left( \sqrt{3}+6\right)}{4}; S = S п о л н = 4 2 a 2 3 + 3 a 2 = 4 2 a 2 ( 3 + 6 ) ;
a 2 = 4 S 2 ( 3 + 6 ) a^2=\dfrac{4S}{2\left( \sqrt{3}+6\right)} a 2 = 2 ( 3 + 6 ) 4 S (Выразим площадь сечения.)
Треугольник Y 1 X Z 1 Y_1XZ_1 Y 1 X Z 1 — равнобедренный, O Y 1 = a 2 ; X Y 1 = a 2 ; OY_1=\dfrac{a}{2}; XY_1=a\sqrt{2}; O Y 1 = 2 a ; X Y 1 = a 2 ;
высота O X = 2 a 2 − a 2 4 = a 7 2 ; OX=\sqrt{2a^2-\dfrac{a^2}{4}}=\dfrac{a\sqrt{7}}{2}; O X = 2 a 2 − 4 a 2 = 2 a 7 ;
S с е ч . = 1 2 ⋅ a ⋅ a 7 2 = a 2 7 4 . S_{сеч.}=\dfrac{1}{2}\cdot a\cdot \dfrac{a\sqrt{7}}{2}=\dfrac{a^2\sqrt{7}}{4}. S с е ч . = 2 1 ⋅ a ⋅ 2 a 7 = 4 a 2 7 .
Подставим формулу a 2 a^2 a 2 в уравнение:
S с е ч . = 4 S ⋅ 7 4 ⋅ 2 ( 3 + 6 ) = S 7 2 ( 3 + 6 ) . S_{сеч.}=\dfrac{4S\cdot \sqrt{7}}{4\cdot 2\left(\sqrt{3}+6\right)}=\dfrac{S\sqrt{7}}{2\left(\sqrt{3}+6\right)}. S с е ч . = 4 ⋅ 2 ( 3 + 6 ) 4 S ⋅ 7 = 2 ( 3 + 6 ) S 7 .
Ответ: S с е ч . = S 7 2 ( 3 + 6 ) . S_{сеч.}=\dfrac{S\sqrt{7}}{2\left(\sqrt{3}+6\right)}. S с е ч . = 2 ( 3 + 6 ) S 7 .