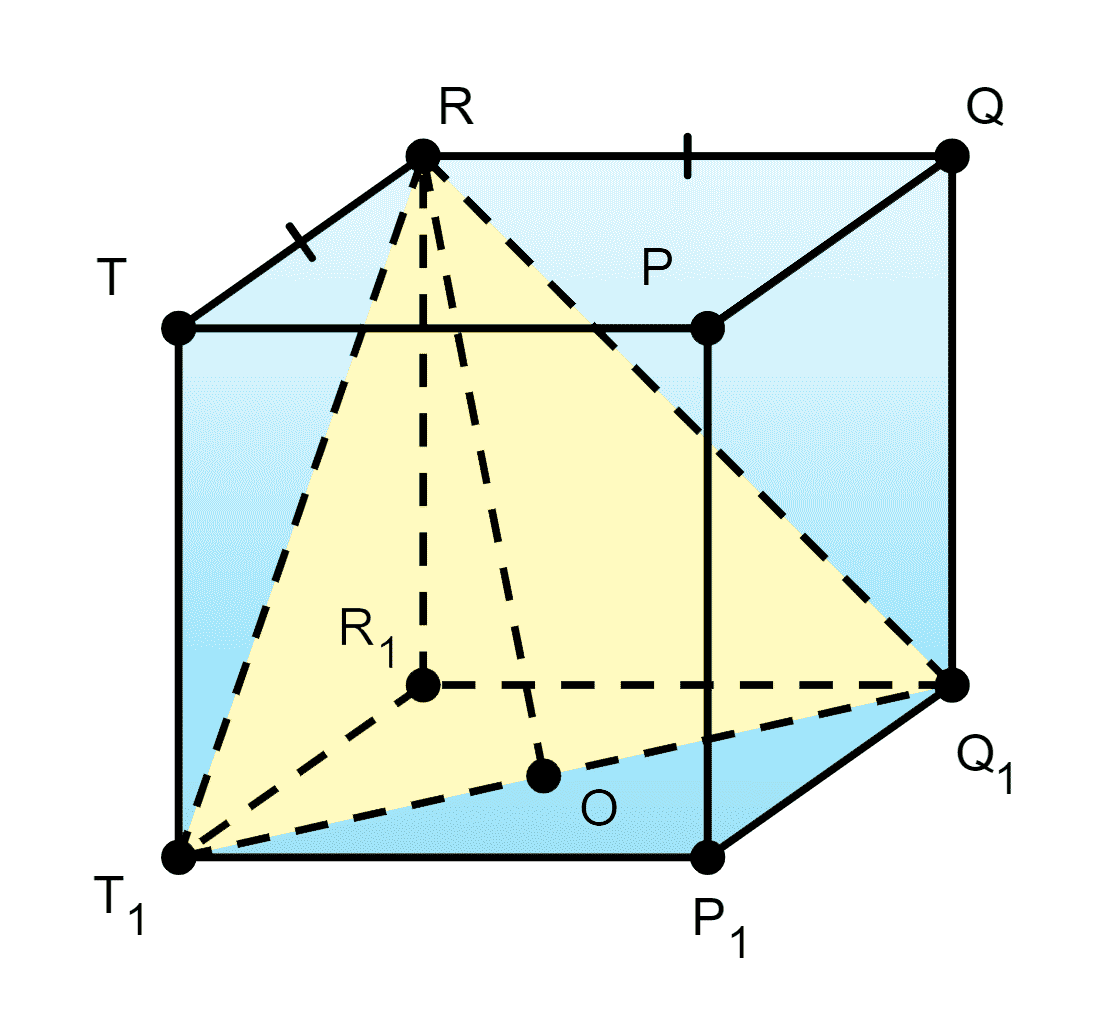
69. Изобразите прямоугольный параллелепипед TPQRT1P1Q1R1 и постройте его сечение плоскостью, которая проходит через прямую T1Q1 и вершину R. Найдите площадь этого сечения, учитывая, что рёбра RT и RQ равны друг ивдругу и равны l, а радиус окружности, описанной около четырёхугольника RQQ1R1, равен a.
Решение:
T 1 R Q 1 T_1RQ_1 T 1 R Q 1 — сечение параллелепипеда плоскостью T 1 R Q 1 ; T_1RQ_1; T 1 R Q 1 ; R T = R Q = l , T P Q R RT=RQ=l, TPQR R T = R Q = l , T P Q R — квадрат; боковые грани — равные прямоугольники с диагоналями, равными 2 a . 2a. 2 a .
По теореме Пифагора T 1 Q 1 2 = T 1 R 1 2 + R 1 Q 1 2 ; T_1Q_1^2=T_1R_1^2+R_1Q_1^2; T 1 Q 1 2 = T 1 R 1 2 + R 1 Q 1 2 ;
T 1 Q 1 = T 1 R 1 2 + R 1 Q 1 2 = l 2 + l 2 = 2 l 2 = l 2 . T_1Q_1=\sqrt{T_1R_1^2+R_1Q_1^2}=\sqrt{l^2+l^2}=\sqrt{2l^2}=l\sqrt{2}. T 1 Q 1 = T 1 R 1 2 + R 1 Q 1 2 = l 2 + l 2 = 2 l 2 = l 2 .
Так как R R Q Q 1 R 1 = a , R_{RQQ_1R_1}=a, R R Q Q 1 R 1 = a , то R Q = 2 a . RQ=2a. R Q = 2 a .
Найдём высоту по теореме Пифагора:
R Q 1 2 = R O 2 + O Q 1 2 ; RQ_1^2=RO^2+OQ_1^2; R Q 1 2 = R O 2 + O Q 1 2 ;
R O = R Q 1 2 − O Q 2 = ( 2 a ) 2 − ( l 2 2 ) 2 = 4 a 2 − 2 l 2 4 = 4 a 2 − l 2 2 . RO=\sqrt{RQ_1^2-OQ^2}=\sqrt{\left( 2a\right)^2-\left( \dfrac{l\sqrt{2}}{2}\right)^2}=\sqrt{4a^2-\dfrac{2l^2}{4}}=\sqrt{4a^2-\dfrac{l^2}{2}}. R O = R Q 1 2 − O Q 2 = ( 2 a ) 2 − ( 2 l 2 ) 2 = 4 a 2 − 4 2 l 2 = 4 a 2 − 2 l 2 .
R O = 4 a 2 − l 2 2 . RO=\sqrt{4a^2-\dfrac{l^2}{2}}. R O = 4 a 2 − 2 l 2 .
Сторона основания треугольника T 1 Q 1 = l 2 . T_1Q_1=l\sqrt{2}. T 1 Q 1 = l 2 .
S T 1 R Q 1 = 1 2 ⋅ T 1 Q 1 ⋅ R O = 1 2 ⋅ l 2 ⋅ 4 a 2 − l 2 2 = l 2 a 2 − l 2 4 . S_{T_1RQ_1}=\dfrac{1}{2}\cdot T_1Q_1\cdot RO=\dfrac{1}{2}\cdot l\sqrt{2}\cdot \sqrt{4a^2-\dfrac{l^2}{2}}=l\sqrt{2a^2-\dfrac{l^2}{4}}. S T 1 R Q 1 = 2 1 ⋅ T 1 Q 1 ⋅ R O = 2 1 ⋅ l 2 ⋅ 4 a 2 − 2 l 2 = l 2 a 2 − 4 l 2 .
Ответ: S T 1 R Q 1 = l 2 a 2 − l 2 4 . S_{T_1RQ_1}=l\sqrt{2a^2-\dfrac{l^2}{4}}. S T 1 R Q 1 = l 2 a 2 − 4 l 2 .