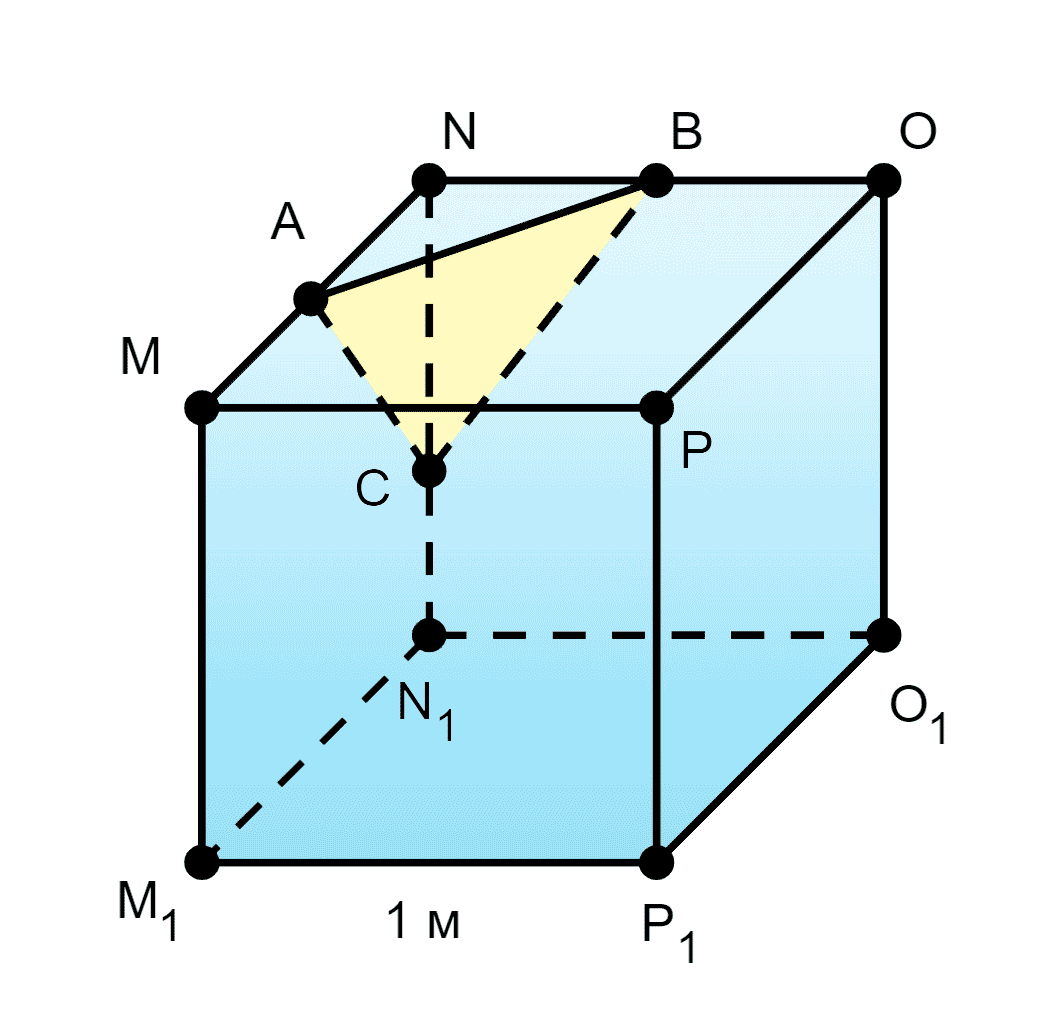
64. Изобразите куб MNOPM1N1O1P1 и отметьте середины A, B и C рёбер NM, NO и NN1. Используя полученный рисунок:

а) постройте сечение куба плоскостью $ABC;$

б) докажите, что треугольник $ABC$ правильный;

в) найдите площадь треугольника $ABC,$ приняв ребро куба равным 1 м.

Решение:

а) $ABC$ — сечение.

б) т.к. $\triangle ANB = \triangle ANC =\triangle BNC,$ (равные прямоугольные треугольники) то их гипотенузы $AB, BC$ и $AC$ тоже равны, значит треугольник $ABC$ — правильный.

в) По теореме Пифагора $AB^2=AN^2+NB^2;$

$AB^2=\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^2=\dfrac{1}{2};$

$AB=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}.$

$S=\dfrac{AB^2\sqrt{3}}{4}=\dfrac{1\cdot\sqrt{3}}{2\cdot 4}=\dfrac{\sqrt{3}}{8}\,(м^2).$

Ответ: $S=\dfrac{\sqrt{3}}{8}\,м^2.$