62. Изобразите куб STRUS1T1R1U1 и отметьте точки B и C на рёбрах SU и RU. Постройте сечение куба плоскостью BCT1.

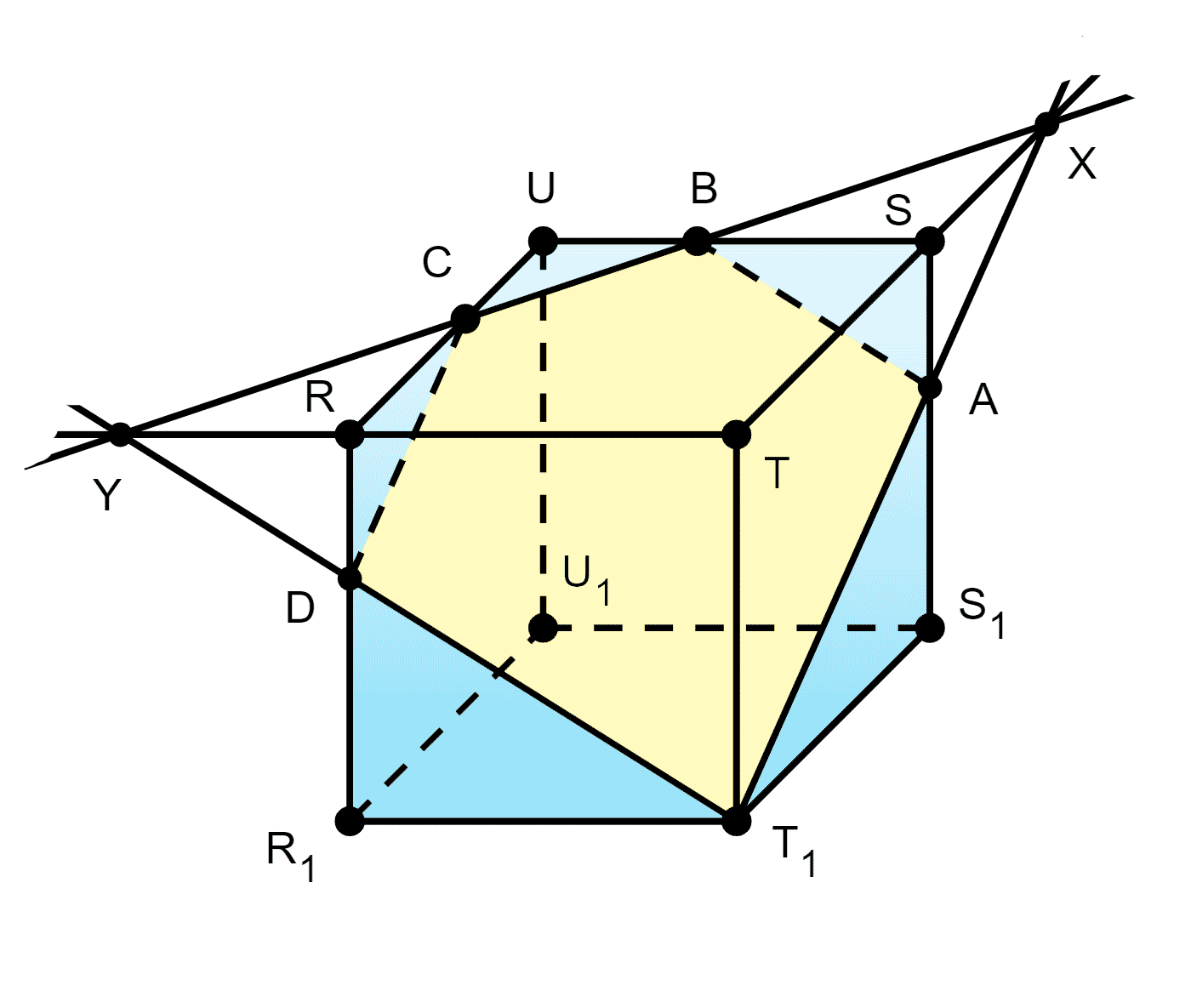
Решение:

Пусть $(BCT_1)=\alpha, \alpha\cap (USTR)=CB$

$CB\cap TS=X; X\subset \alpha; X\in (TSS_1T_1)$

$XT_1\cap SS_1=A; T_1\subset\alpha; T_1\in (TSS_1T_1)$

$\alpha \cap (U_1USS_1)=AB$

$\alpha \cap (T_1TSS_1)=AT_1$

Аналогично находим $DT_1=\alpha \cap (R_1RTT_1)$ и $CD=\alpha\cap (R_1RUU_1)$

$ABCDT_1$ — искомое сечение.