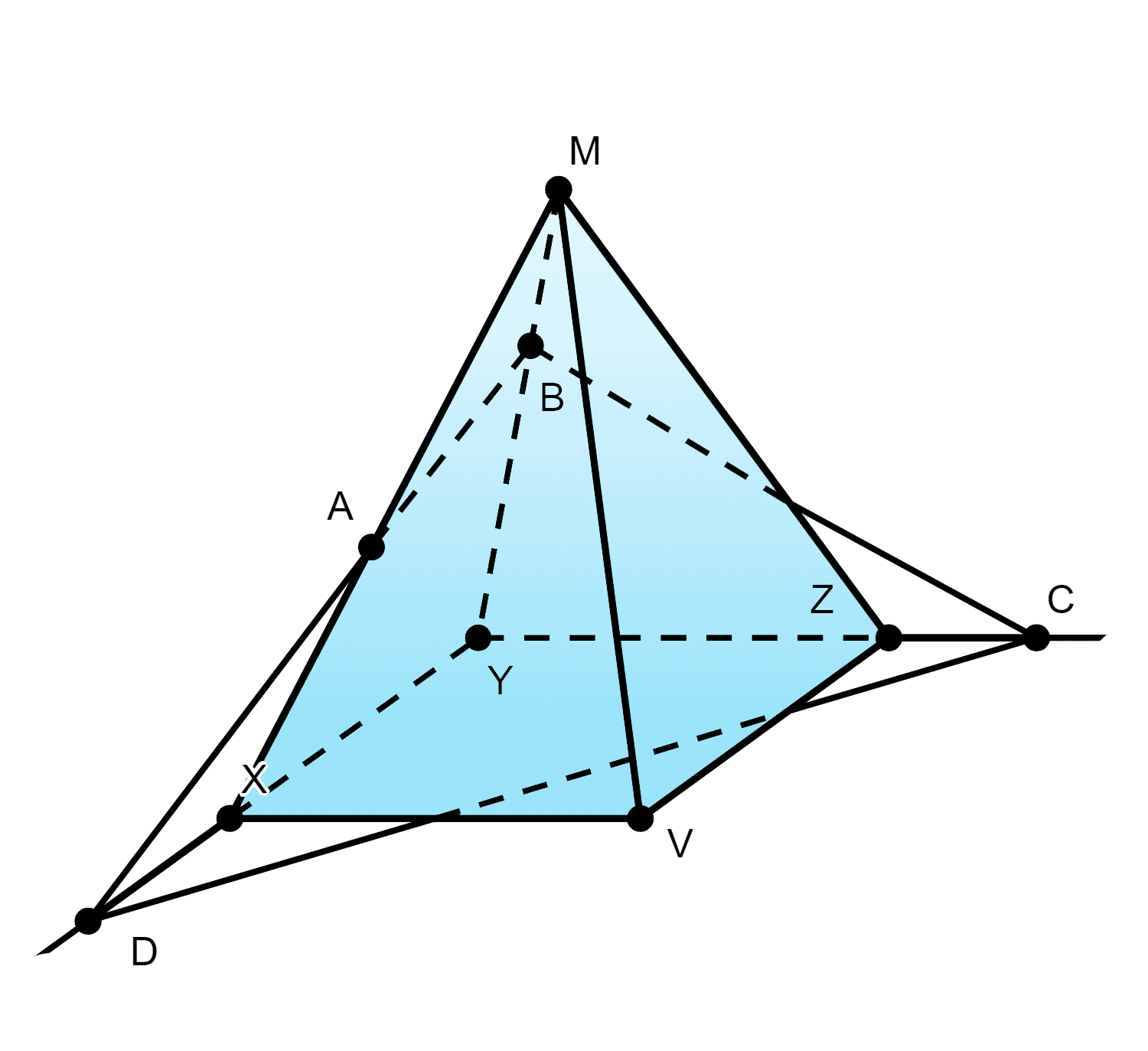
56. Выберите точки A и B соответственно на рёбрах MX и MY четырёхугольной пирамиды MXYZV, а точку C — на луче YZ за точкой Z. Постройте прямую, по которой пересекаются плоскости ABC и XYZ.

Решение:

$MXYZV$ — четырёхугольная пирамида;

$A\in MX; B\in MY; C\in YZ.$

$(YMZ)\cap (XYZ)=YZ=YC \Rightarrow C\in (XYZ): C\in (ABC).$

$(XMV)\cap (XYZ)=YX=YD.$

$D\in (XYZ); D\in (ABC),$ т.к. $D\in AB$ по Аксиоме 2,

$CD=(ABC)\cap (XYZ).$