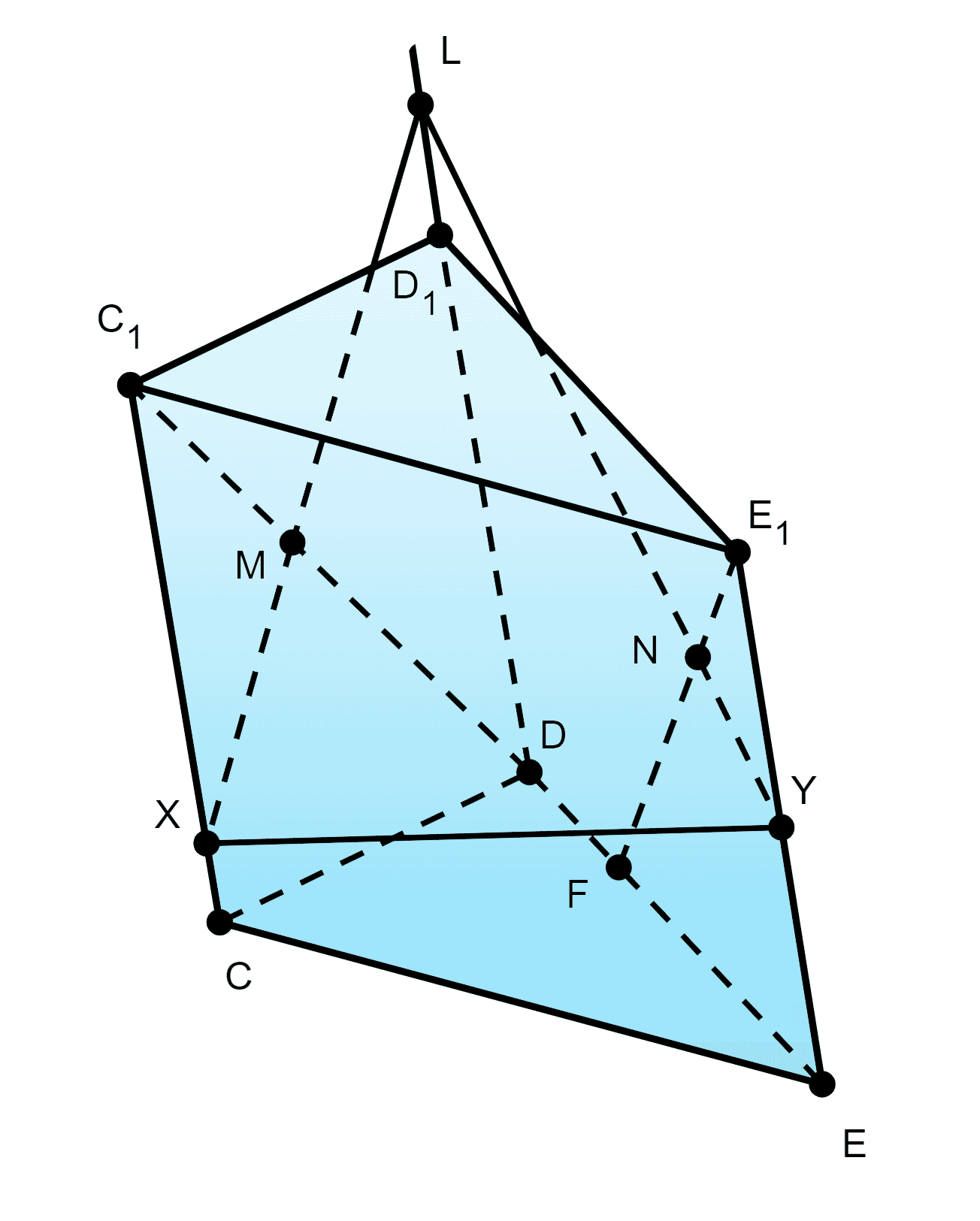
55. Точку M выберите на диагонали DC1 грани треугольной призмы CDEC1D1E1, точку N — на отрезке E1F, где F — внутренняя точка ребра DE, точку L — на луче DD1 за точкой D1 (рис. 100). Постройте прямую, по которой плоскость MNL пересекает плоскость ECC1.

Решение:

В грани $CC_1D_1D$ проведём прямую $ML,$ тогда $ML\cap C_1C=X.$

В грани $DD_1E_1E$ проведём прямую $LN,$ тогда $NL\cap EE_1=Y.$

$X\in (EC_1C)$ и $Y\in (EC_1C).$

По Аксиоме 2 $XY\subset (EC_1C),$ значит

$(ECC_1)\cap (MNL)=XY, (MNL)=(XLY).$