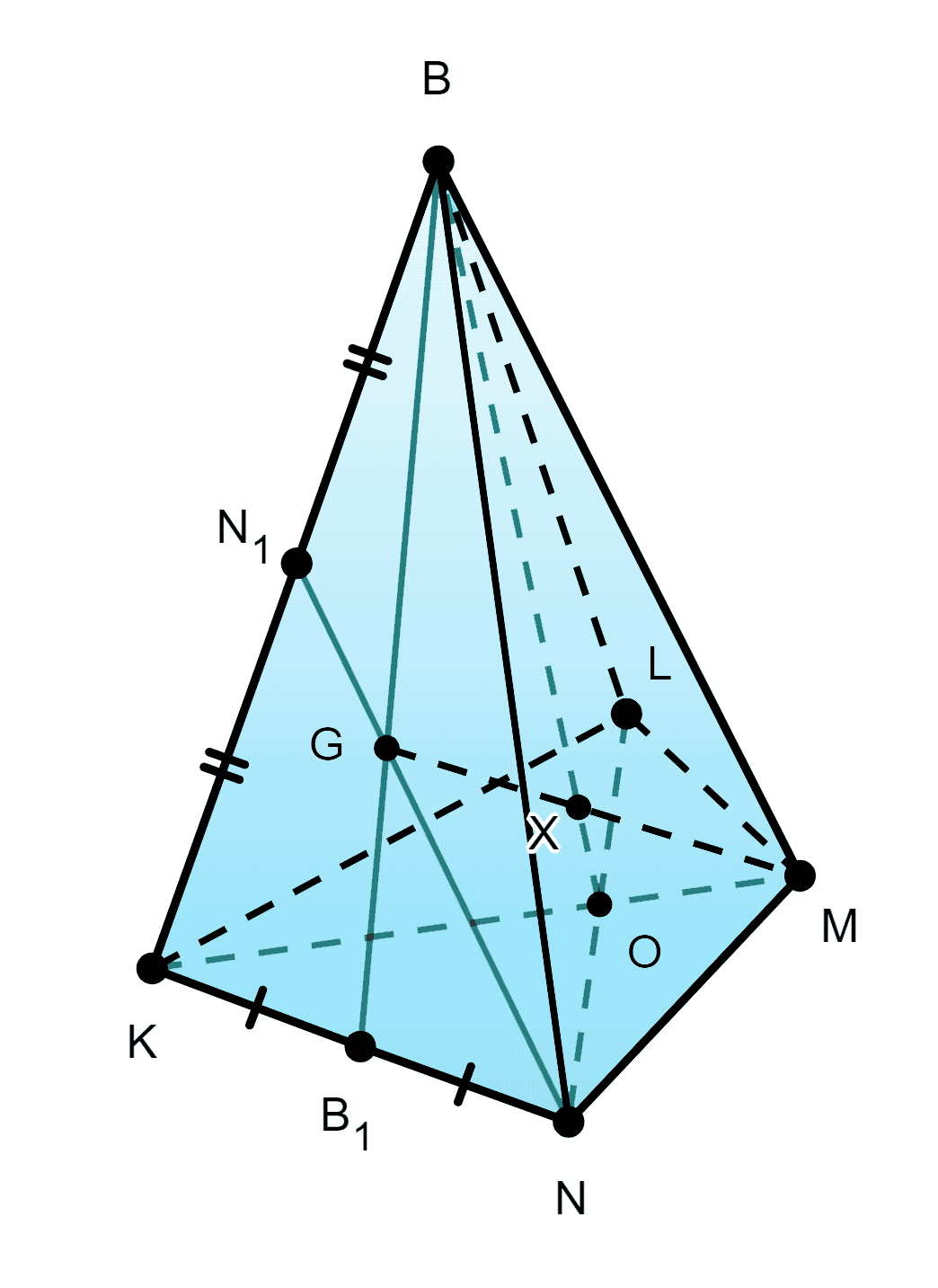
54. Медианы BB1 и NN1 грани BKN четырёхугольной пирамиды BKLMN пересекаются в точке G (рис. 99). Сделайте такой рисунок в тетради и постройте точку, в которой прямая MG пересекает плоскость BLN.

Решение:

Строим точку, которая пересекает диагонали основания $O=KM\cap LN,$ проводим прямую $BO$ и прямую $MG,$ находим $X=MG\cap BO,$ $X=MC\cap (BLN).$ Прямая $MG$ пересекает плоскость $BLN$ в точке $X.$