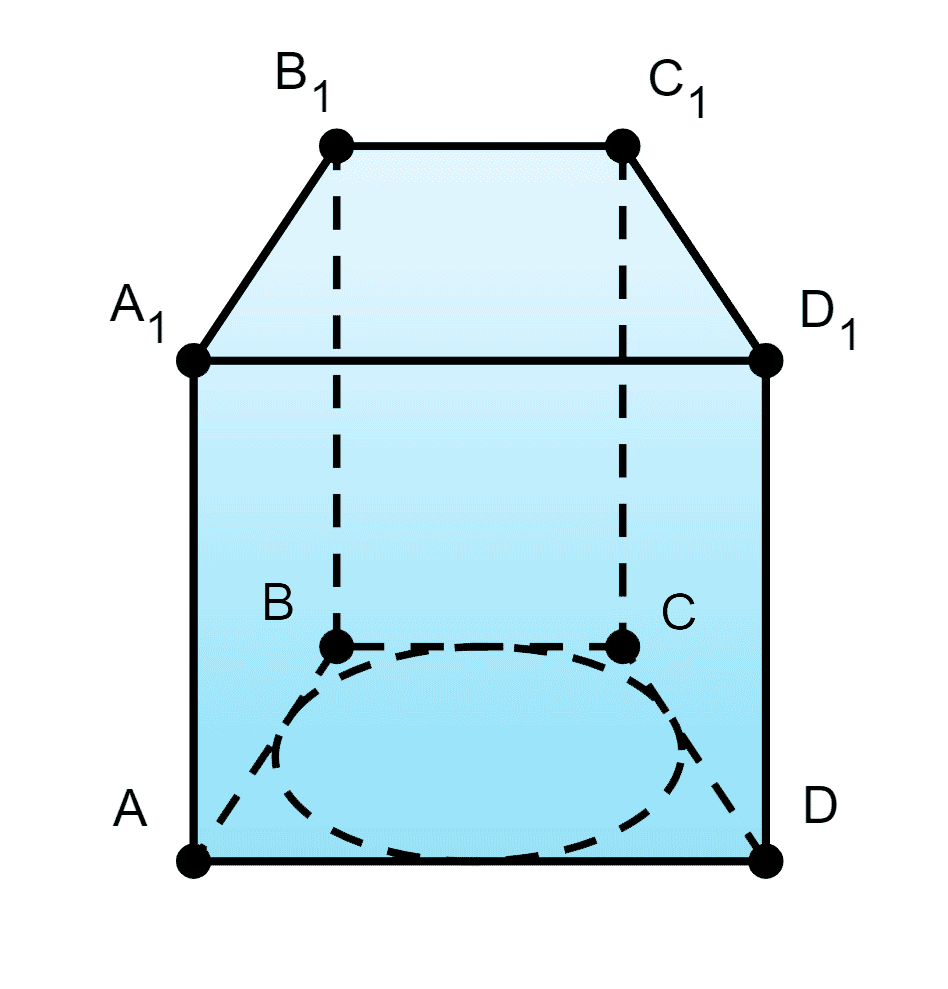
53. Основанием прямой призмы является равнобедренная трапеция, в которую можно вписать окружность. Боковая сторона трапеции равна 12 см и образует с основанием угол в 30°. Найдите боковое ребро призмы, учитывая, что её полная поверхность равна 336 см^2 .

Решение:

ABCDABCD — равнобедренная трапеция, в которую можно вписать окружность, AB=12 см,∠A=30°.AB=12\,см, \angle{A}=30°. Sполн=336 см2.S_{полн}=336\, см^2.

Найдём периметр основания PоснP_{осн} и площадь основания Sосн.S_{осн}.

Для данной трапеции справедливы формулы: высота h=2r,h=2r, AB+CD=BC+AD;Sосн=p⋅rAB+CD=BC+AD; S_{осн} = p\cdot r (произведение полупериметра и радиуса вписанной окружности); P=4AB.P=4AB.

Таким образом h=122=6h=\dfrac{12}{2}=6 (см) (катет, лежащий против угла в 30° равен половине гипотенузы);

r=h2=62=3r=\dfrac{h}{2}=\dfrac{6}{2}=3 (см);

P=4⋅12=48P=4\cdot 12=48 (см),

p=P2=482=24p=\dfrac{P}{2}=\dfrac{48}{2}=24 (см);

Sосн=24⋅3=72S_{осн}=24\cdot 3=72 (см2);(см^2);

Sбок=Sполн−2Sосн=336−2⋅72=192 (см2).S_{бок}=S_{полн}-2S_{осн}=336 - 2\cdot 72=192\, (см^2).

Боковое ребро AA1=Sбокp=19248=4 см.AA_1=\dfrac{S_{бок}}{p}=\dfrac{192}{48}=4\, см.

Ответ: 4 см.4\, см.