52. Основанием прямой треугольной призмы является прямоугольный треугольник, радиусы вписанной в него и описанной около него окружностей равны соответственно 4 см и 10 см. Найдите полную поверхность призмы, учитывая, что её боковое ребро равно 16 см.

Решение:

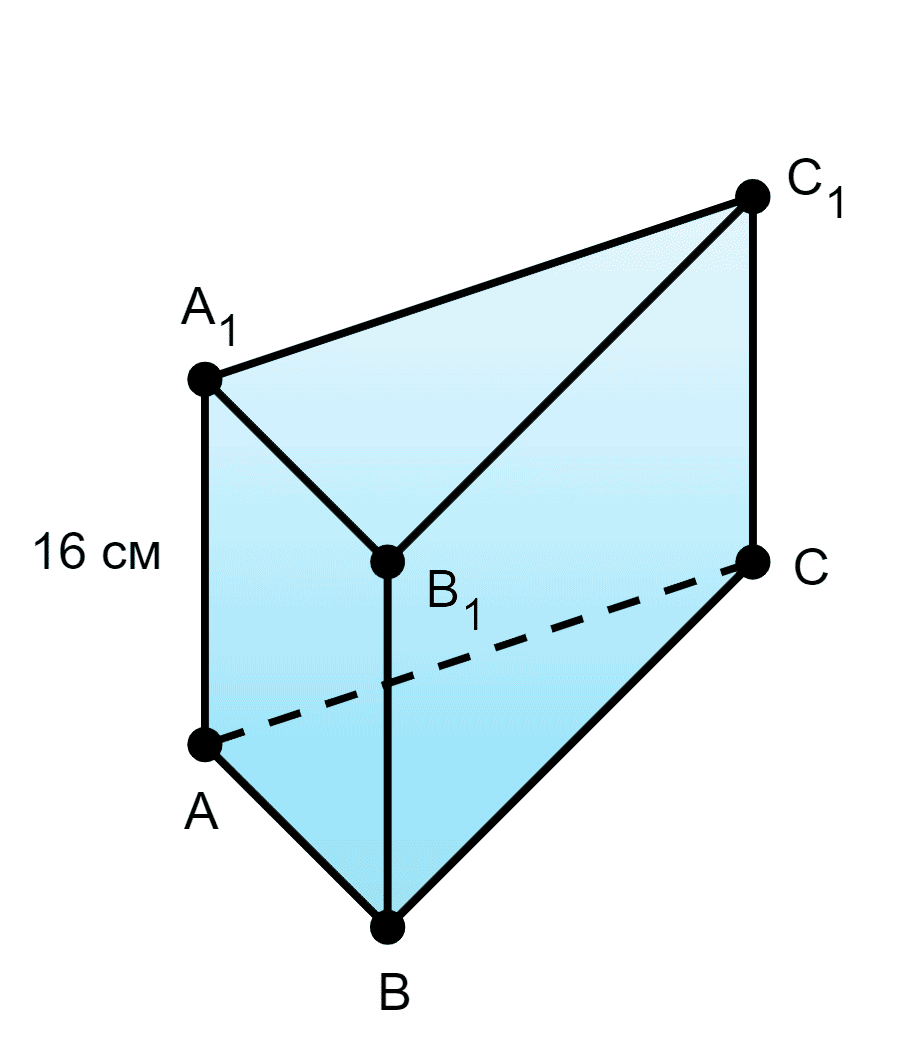
Пусть ABCA1B1C1ABCA_1B_1C_1 — прямая треугольная призма, основание — прямоугольный треугольник, у которого rr — 4 см, RR — 10 см, AA1=16 см.AA_1=16\,см.

Применим формулы r=pABC−AC;AC=2R,S=pABC⋅r,r=p_{ABC}-AC; AC=2R, S=p_{ABC}\cdot r, где полупериметр p=AB+BC+AC2,p=\dfrac{AB+BC+AC}{2}, rr — радиус вписанной окружности, RR — радиус описанной окружности. Таким образом гипотенуза AC=2R=20 см;4=p−20,p=24 см;P=48 см,Sосн=p⋅r=24⋅4=96 см2;Sбок=P⋅AA1=48⋅16=768 см2.AC=2R=20\,см; 4=p-20, p=24\,см; P=48\,см, S_{осн}=p\cdot r=24\cdot 4=96\,см^2; S_{бок}=P\cdot AA_1=48\cdot 16=768\,см^2.

Sполн=Sбок+2Sосн;S_{полн}=S_{бок}+2S_{осн};

Sполн=768+192=960 см2.S_{полн}=768+192=960\,см^2.

Ответ: 960 см2.960\, см^2.